914 字
5 分钟
【概统】第四章整理
条件数学期望、协方差矩阵不考
目录
Tips of this Chapter:
- 有些积分,注意分部积分法的使用。常见如多项式乘e指数的运算。
- 关于一般正态分布的运算,经常转换为标准正态分布计算。假设变量,其服从标准正态分布。进行相关运算后,再利用逆线性变换将的相关值转化到目标变量的相关值。
常见随机变量的数字特征
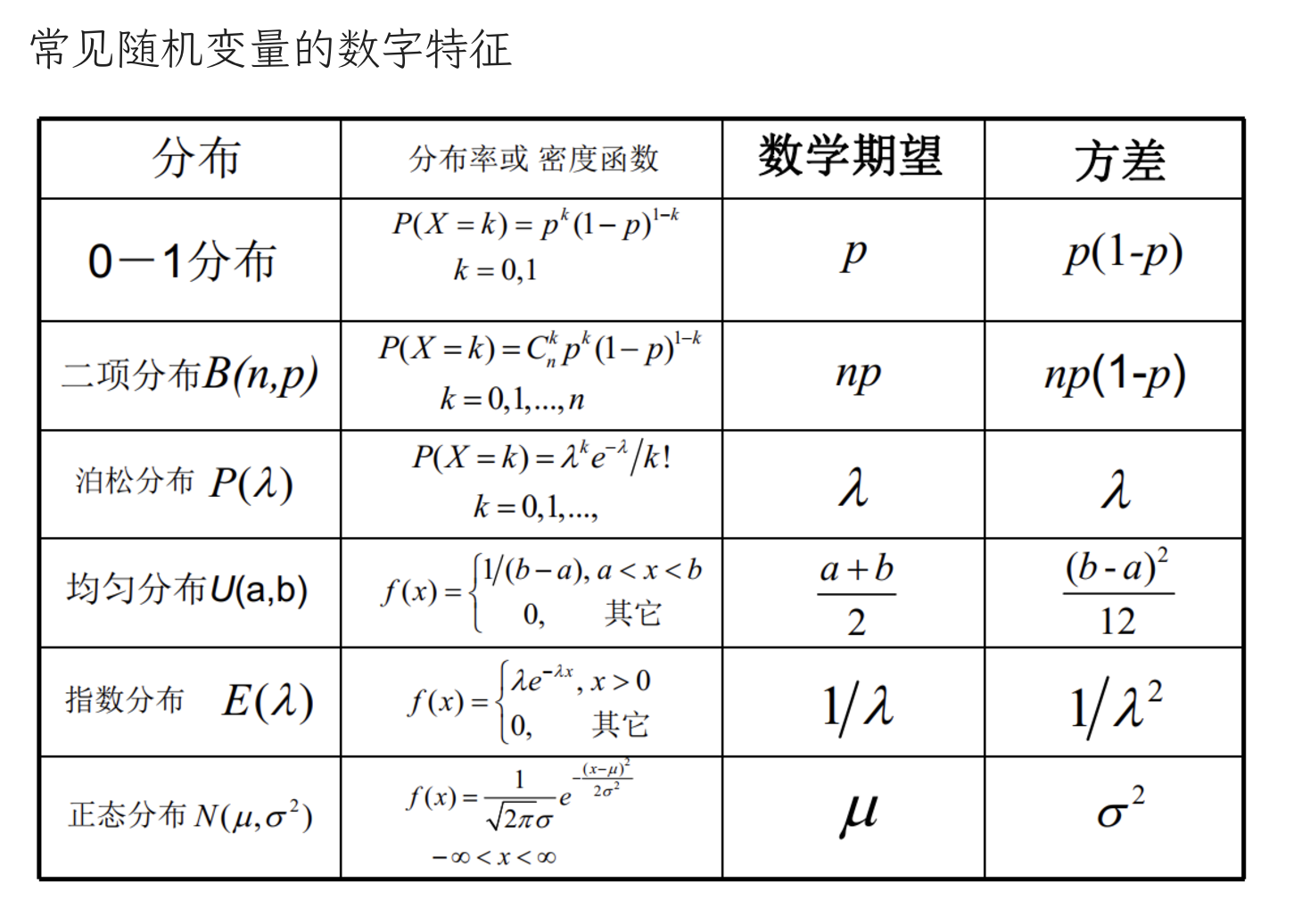
数学期望
随机变量的数学期望
又称期望、均值。
定义
- 离散型
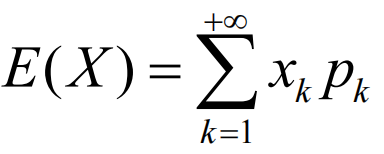 有期望的前提:
有期望的前提: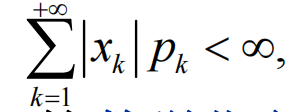
- 连续型
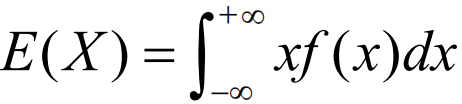 有期望的前提:
有期望的前提: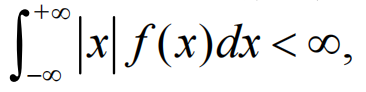
小结论:
- 若 ~ (泊松分布),则
- 若 ~ (指数分布),则
随机变量函数的数学期望
定理

 定理的意义:求E(Y)时,不必算出Y的分布律或概率密度函数,只利用X的分布律或概率密度函数。
定理的意义:求E(Y)时,不必算出Y的分布律或概率密度函数,只利用X的分布律或概率密度函数。
数学期望的性质

 一种解题方法:找到目标变量所代表的函数(进行拆解)
一种解题方法:找到目标变量所代表的函数(进行拆解)  < details 答案 >
< details 答案 >

< /details > 
方差
定义

- 离散型:
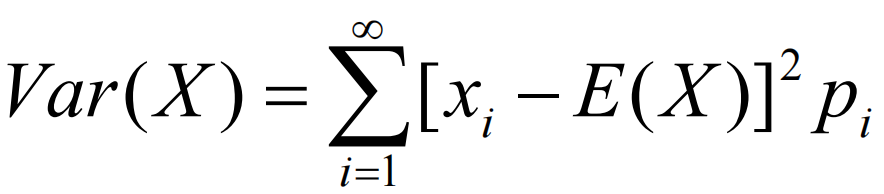
- 连续型:
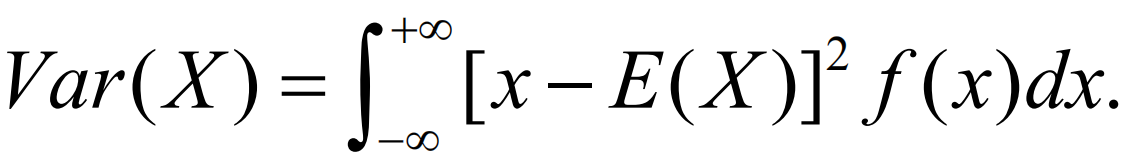
- 方差的性质:
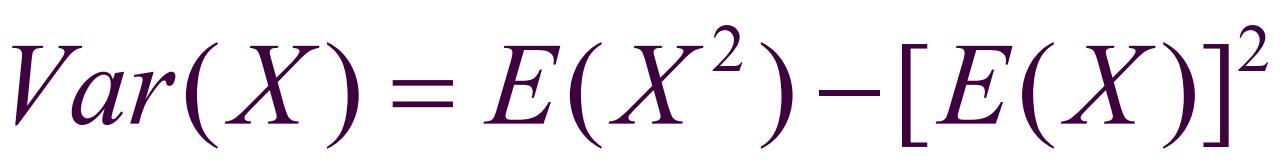
关于分布律的结论
- 泊松分布:若 ~ ,则均值和方差都是
- 均匀分布:若 ~ ,那么均值为 ,方差为
- 二项分布:若 ~ ,则
- 正态分布:若 ~ ,则
- 标准正态分布(概率密度为 ,可以推出后面的和一些中间结论):
- 独立的n个正态变量的线性组合仍服从正态分布:

方差的性质


标准化变量
定义

协方差
定义、计算公式、方差性质补充
 方差性质的补充公式,可以和相互独立的情况比较(多了一个)
方差性质的补充公式,可以和相互独立的情况比较(多了一个)
协方差性质
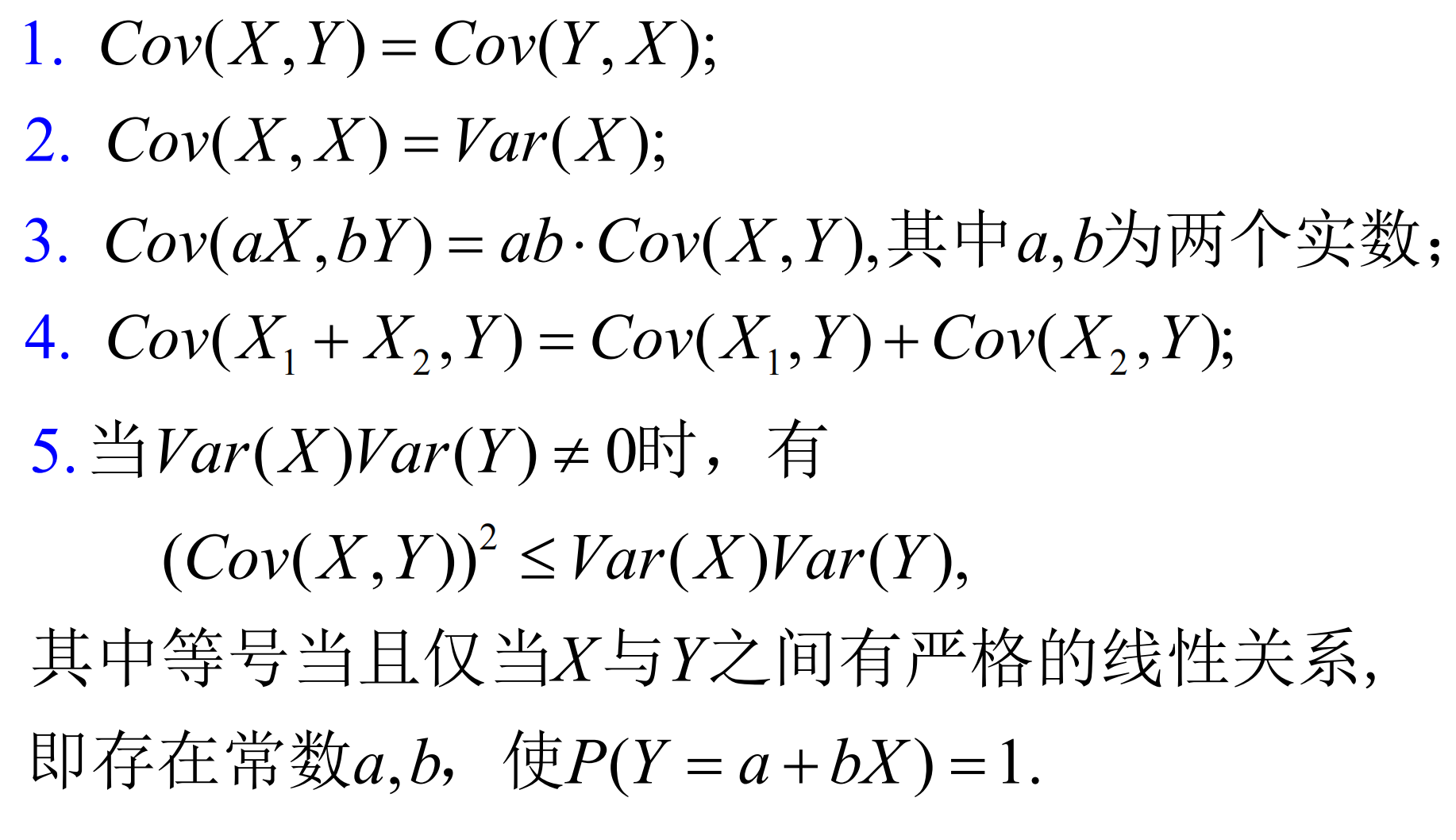 几个小结论,可以推推看:
几个小结论,可以推推看: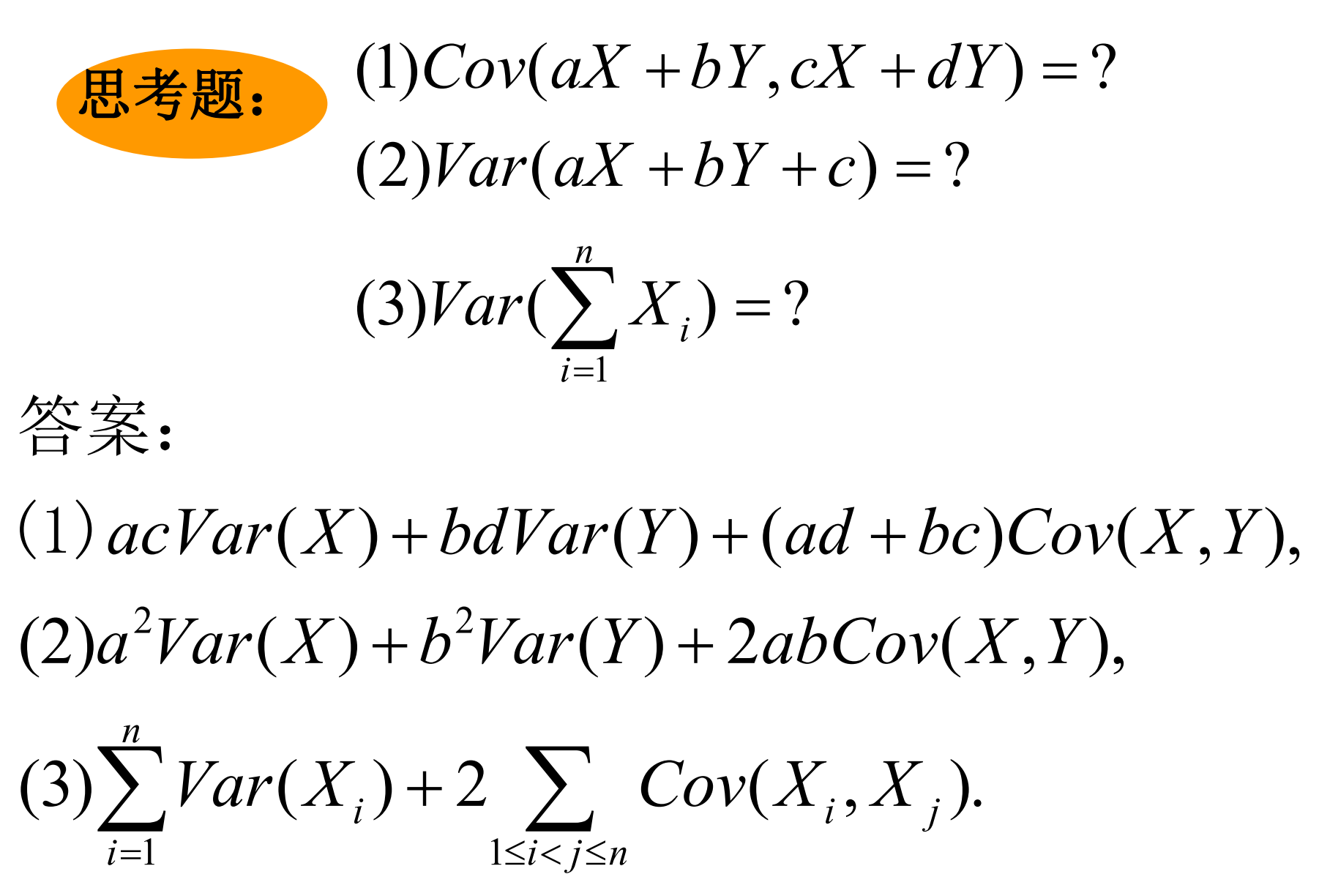
相关系数
定义
 Q:第二个公式有啥用?
Q:第二个公式有啥用?
相关系数的性质
 < details 拓展部分,初次复习可略过 >
< details 拓展部分,初次复习可略过 >
(拓展?)均方误差 

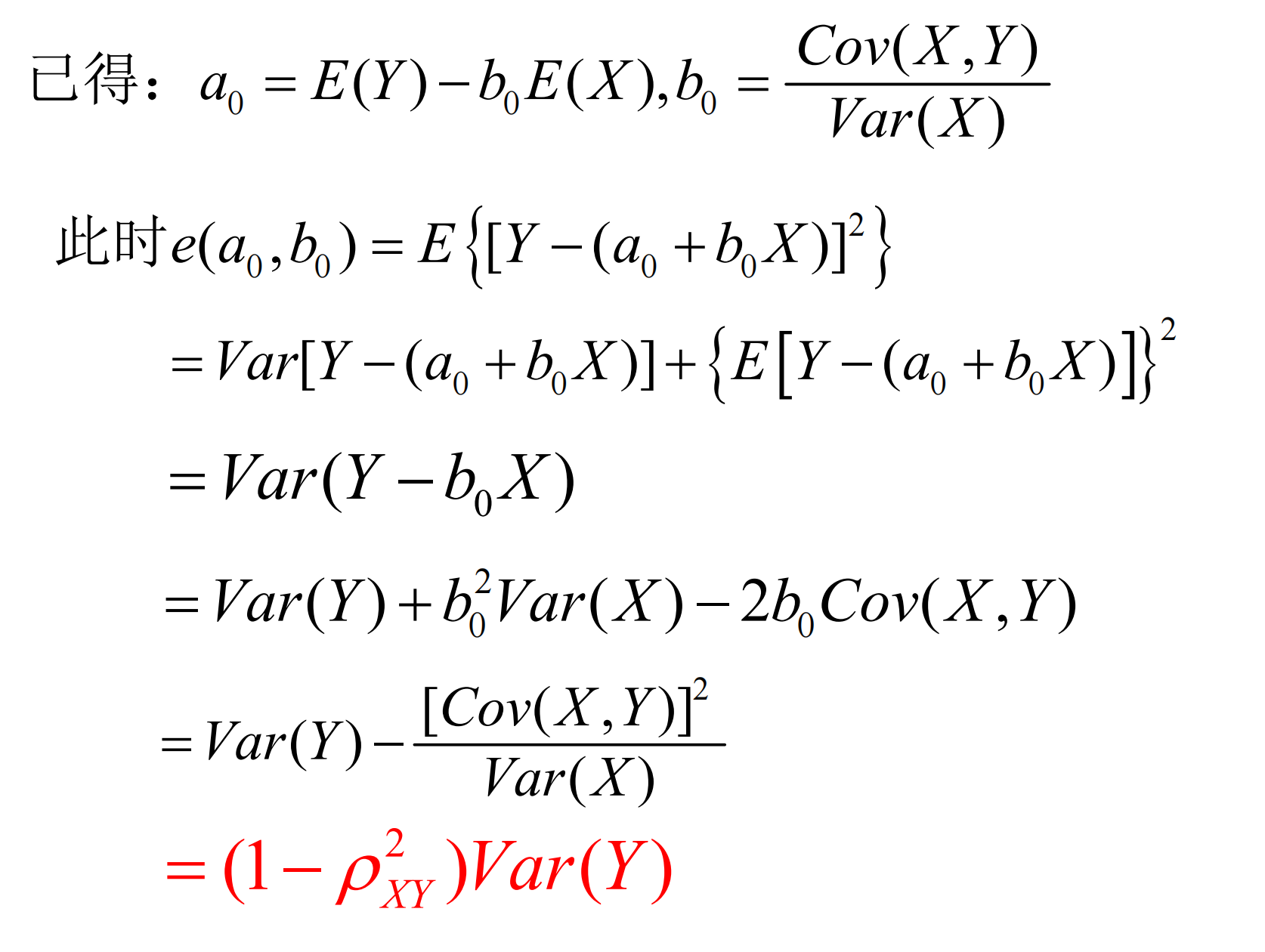
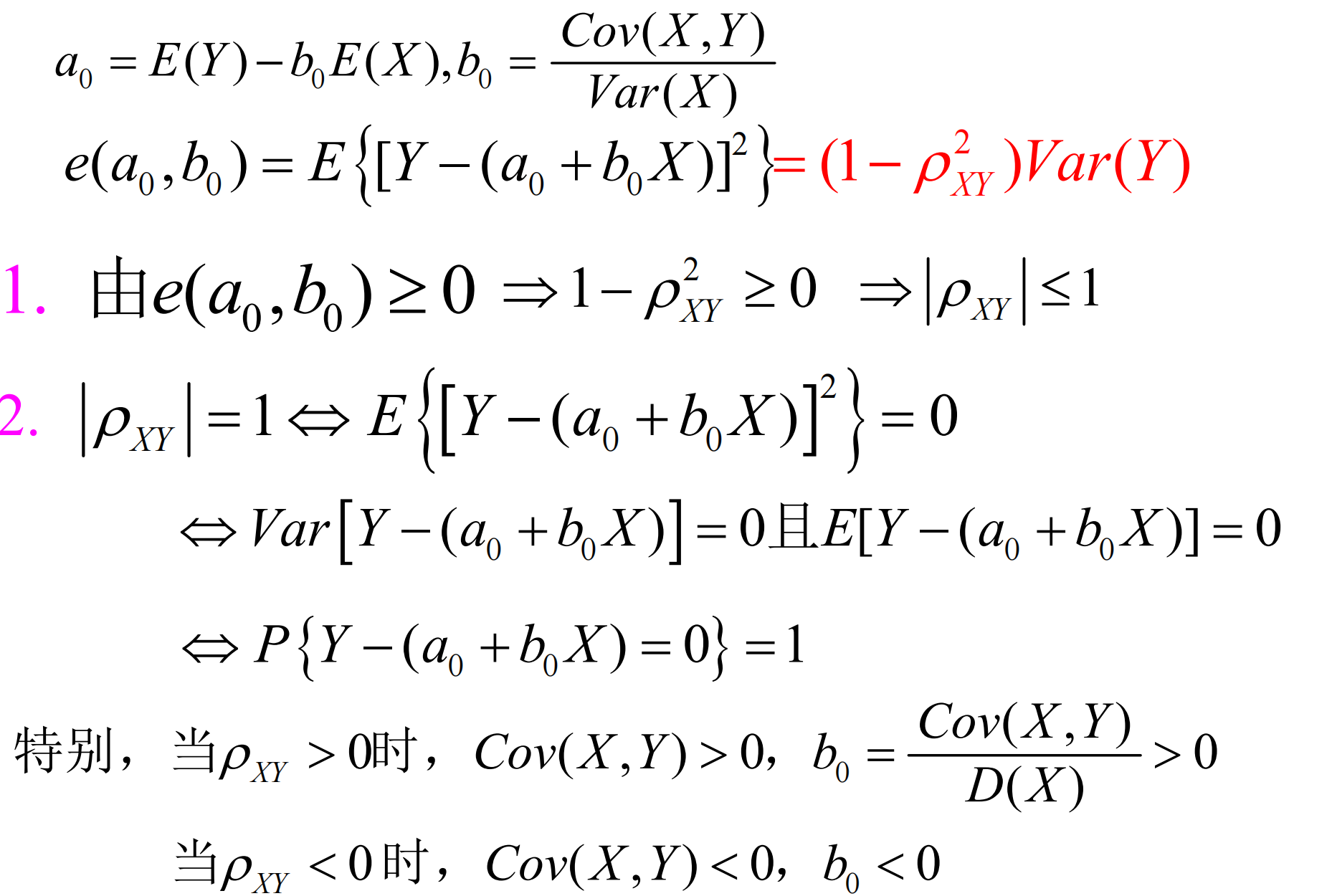
< /details >
相关系数的意义、相关性

不相关或零相关
 区别:相关性与独立性的判断
区别:相关性与独立性的判断
结论:二元正态分布的相关系数

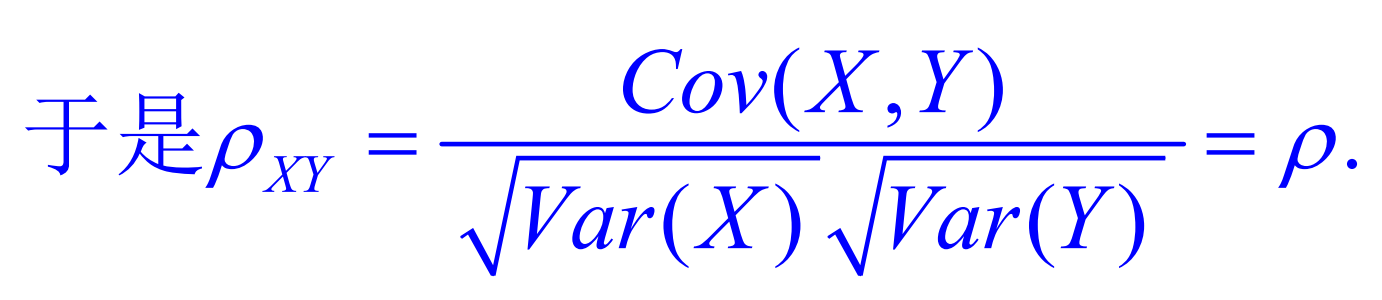

其他数字特征
k阶矩

上(侧)α分位数
 注意不等号。
注意不等号。 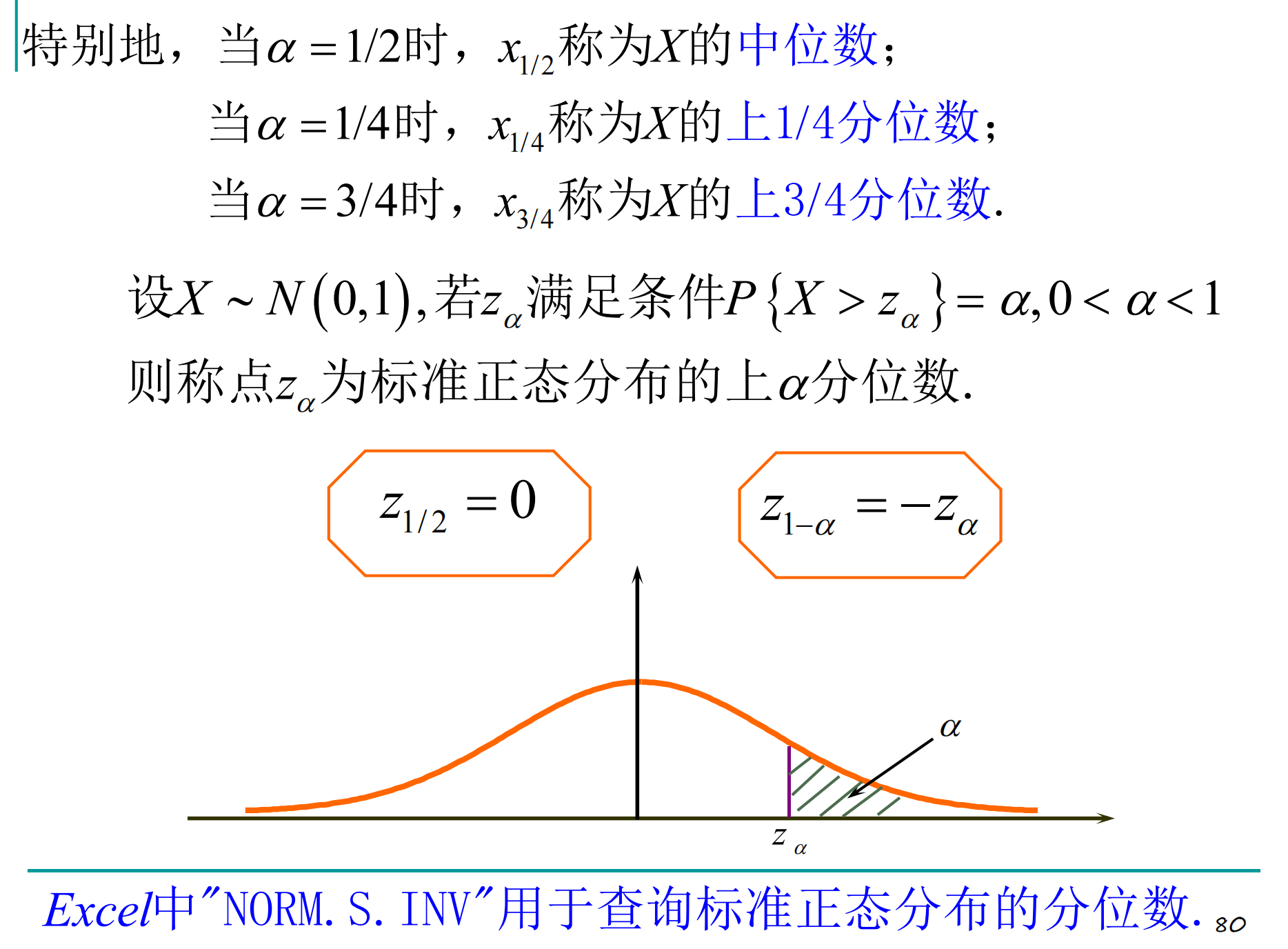
多元随机变量的数字特征
1. n元随机变量的数学期望(向量)
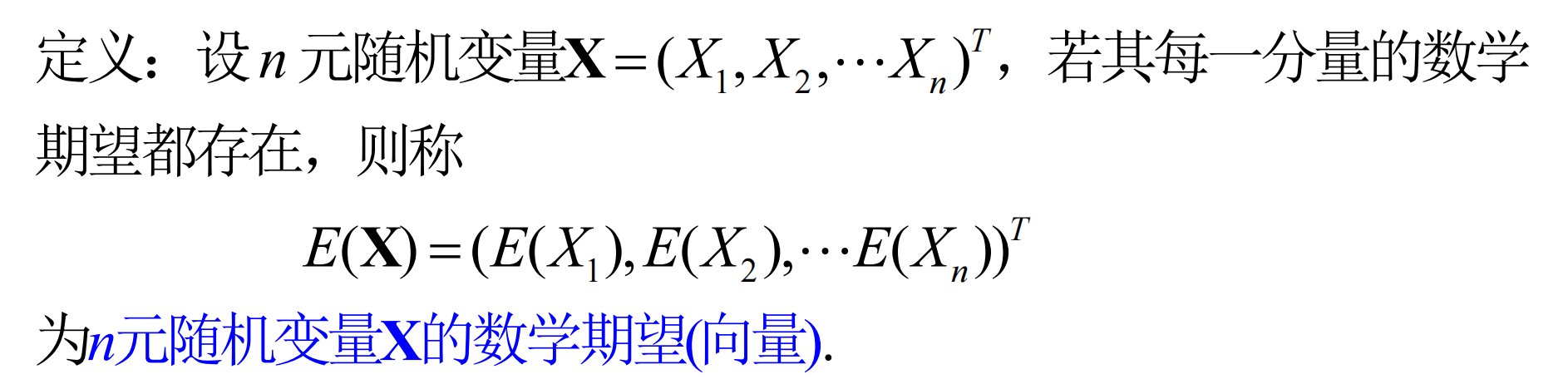
2. 协方差矩阵


n元正态变量有关
n元正态变量的概率密度
利用协方差矩阵,可由二元正态变量的概率密度推广,得到n元正态变量的概率密度: 
n元正态变量 四条重要性质



