目录
第一章
的条件是相互独立 的条件是互斥 不然就要用容斥原理!把每个事件要表示清楚!
不相容=互斥≠对立 区分!
例题:注意第二小问 


贝叶斯/全概率:由果溯因的方法(贝叶斯方法)
- 最大后验概率准则
第二章
离散型随机变量及其分布
- 离散型随机变量的分布律:

明确几种随机变量分布的定义: (注意:概率公式、自变量范围、服从的参数、概率随自变量的变化图线)
随机变量的分布函数
- 连续型随机变量的分布律定义:

分布函数:
- 定义:小于等于x的概率
- 性质:
 说明:
说明:- 性质2:注意右边等号,左边不等
- 性质3:理解:分布函数为什么右连续?如图:
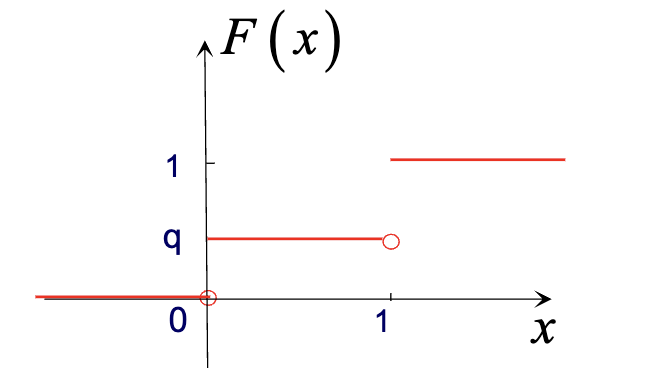
- 性质4:

连续型随机变量及其密度函数
- 连续型随机变量X的定义:(概率)密度函数和分布函数的关系
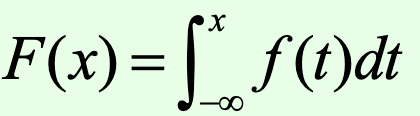
密度函数
- f(x)性质:
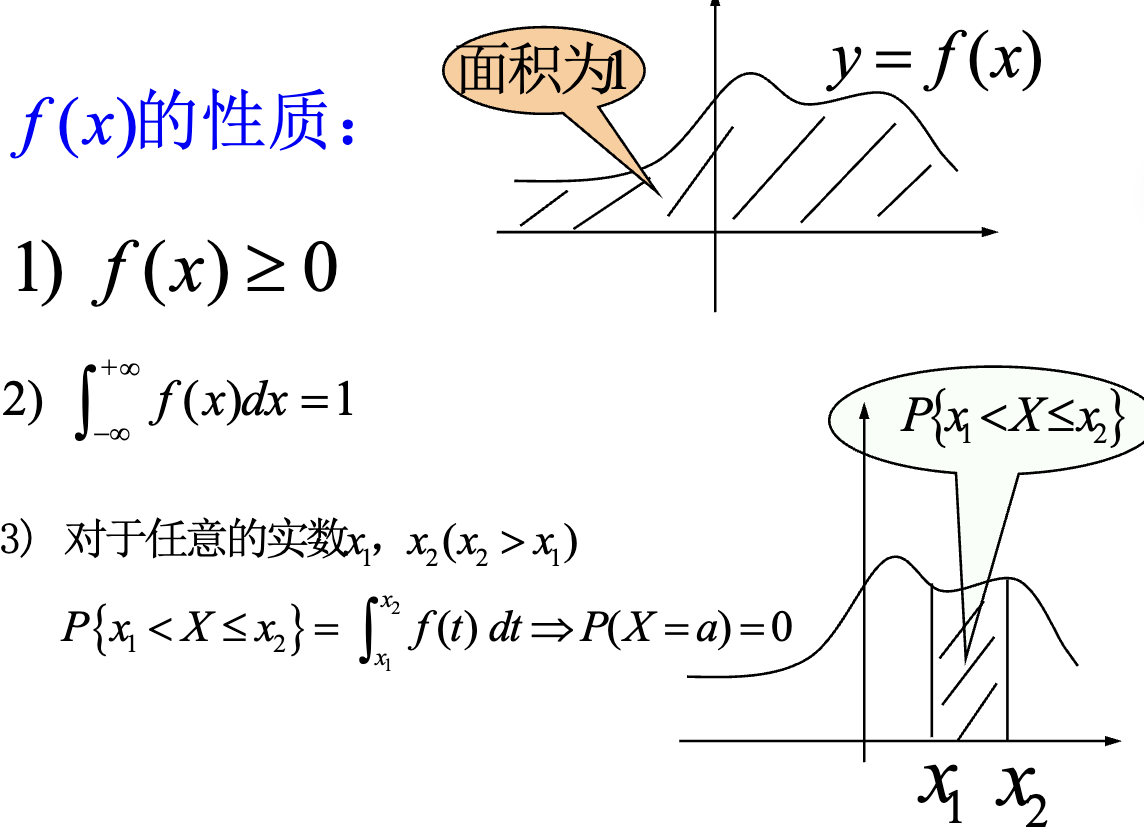

1.离散型随机变量分布
0-1分布
(掷一次骰子)1重贝努力实验
二项分布
n重贝努力实验
泊松分布
单位时间内独立事件发生次数的概率分布
- 公式:


- 应用 && 性质(与二项分布的近似关系、条件):

超几何分布
不放回取样
几何分布
在一系列独立的伯努利试验中,第一次成功发生前所需的试验次数。
试验次数表示第次试验首次成功。
巴斯卡分布
 表示在 k-1 次试验中选出 r-1 次成功的方式数。(第k次实验才获得r次成功的概率)
表示在 k-1 次试验中选出 r-1 次成功的方式数。(第k次实验才获得r次成功的概率)
下面描述的V服从巴斯卡分布:
2.连续型随机变量分布
均匀分布
区间(a,b)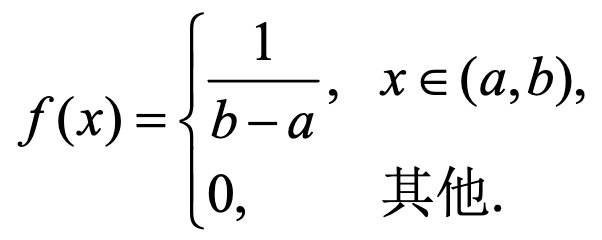 得出:
得出: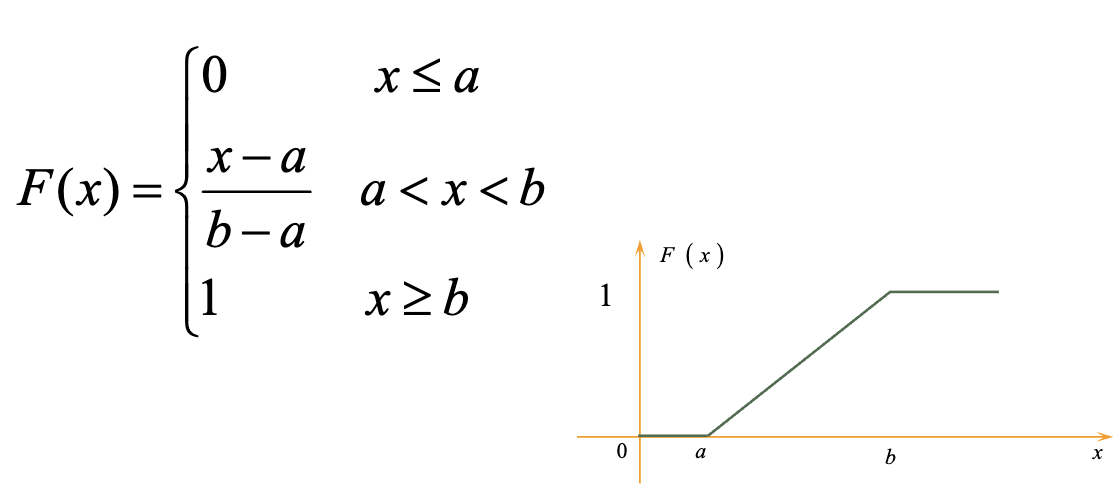
例题: 注意第二小问,不是0.6!(两个事件概率相乘之前,要判断是否相互独立!否则需要利用容斥原理减去重叠值)
注意第二小问,不是0.6!(两个事件概率相乘之前,要判断是否相互独立!否则需要利用容斥原理减去重叠值) 
指数分布
- 定义
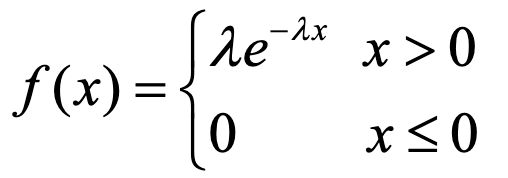
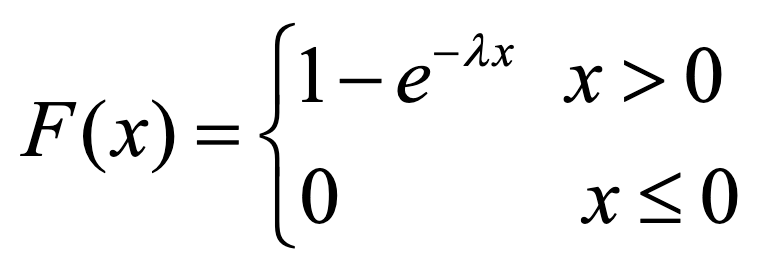
- 性质:具有无记忆性
 (注意不等号的方向!!)
(注意不等号的方向!!)
正态分布/Gauss分布
定义:

性质:
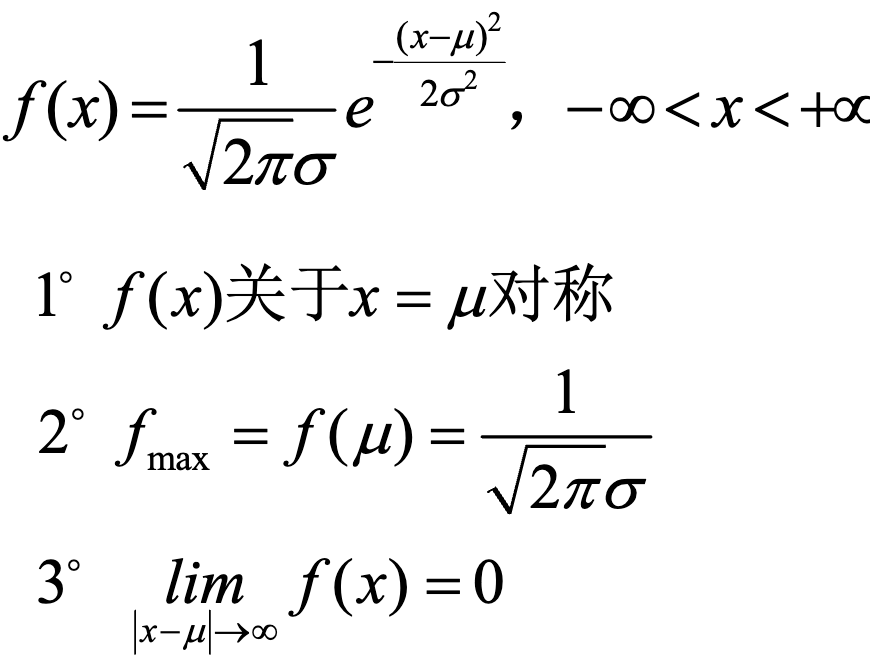 σ越小,图形越高越瘦;σ越大,图形越矮越胖。 称μ为位置参数(决定对称轴位置)σ为尺度参数(决定曲线分散性)。
σ越小,图形越高越瘦;σ越大,图形越矮越胖。 称μ为位置参数(决定对称轴位置)σ为尺度参数(决定曲线分散性)。标准正态分布:Z ~ N(0,1)
- 分布函数函数有如下结论(面积代表分布函数,曲线代表概率密度):
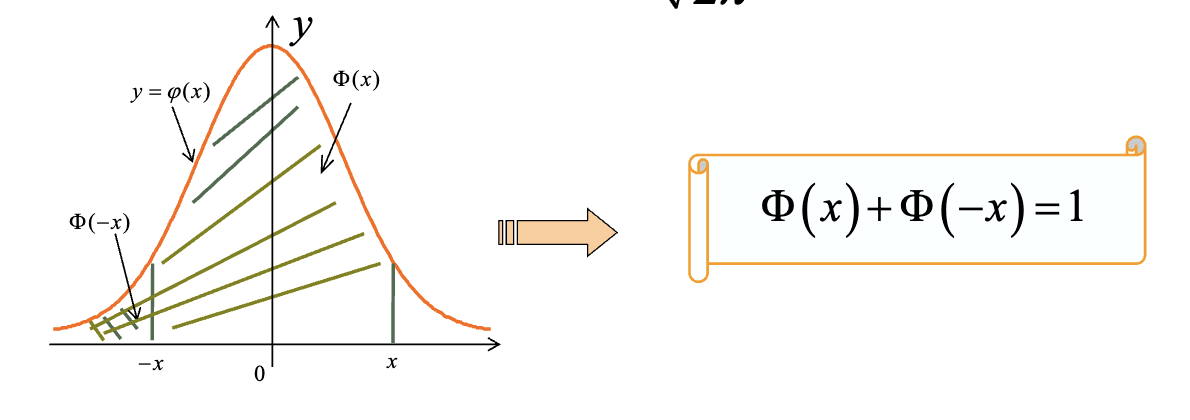
- 变换(套用标准正态分布的分布函数):
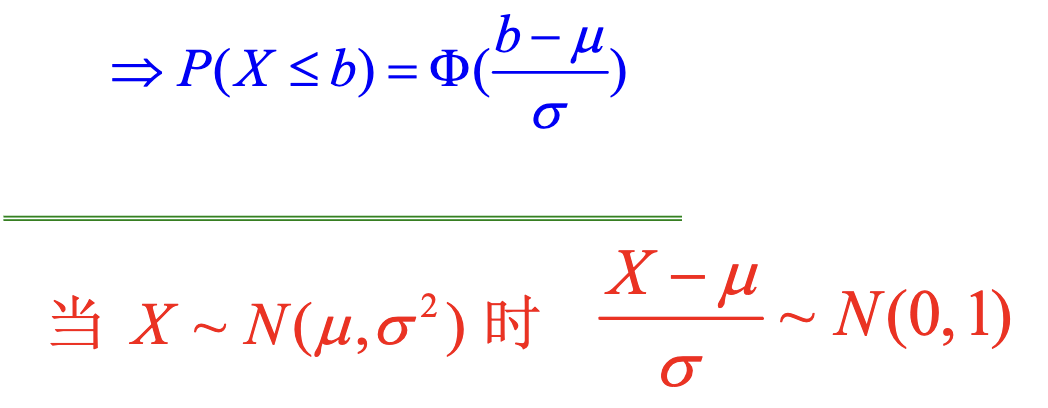
- 分布函数函数有如下结论(面积代表分布函数,曲线代表概率密度):
正态分布的分布函数是f(x)的超越积分(不可积积分),它的原函数是非常规的。但是可以通过平方的形式,求其定积分,如:

3σ法则:0.6826 0.9655 0.9974
正态分布题目:有时候画图会很方便理解做题
注意:离散型随机变量的要求是,变量在离散的点上取到。连续型随机变量的要求是,变量在任意一个值的概率均为0。 举例: 观察到Y=15点的分布函数不连续,再利用
观察到Y=15点的分布函数不连续,再利用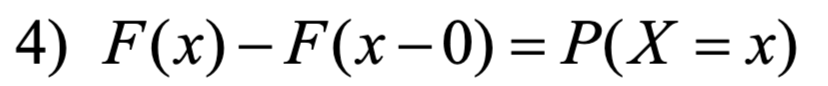 得到X=15处概率P不为0,所以不是连续型随机变量。 推论:连续型随机变量的分布函数在定义域上内闭一致连续。
得到X=15处概率P不为0,所以不是连续型随机变量。 推论:连续型随机变量的分布函数在定义域上内闭一致连续。
随机变量函数的分布
解题方法
寻找变量x与变换后变量y,从y化归到x的条件求解。
- 离散型:可能取值、等价事件 -> 概率分布
- 连续型:Y的概率分布函数、等价事件 ->y 的概率密度函数

 这里的h是x关于y的反函数。(不要忘记是对y求导,不是x,内部的复合函数也要注意求导出来)
这里的h是x关于y的反函数。(不要忘记是对y求导,不是x,内部的复合函数也要注意求导出来)
两个结论:(建议自己会推)
(1) 
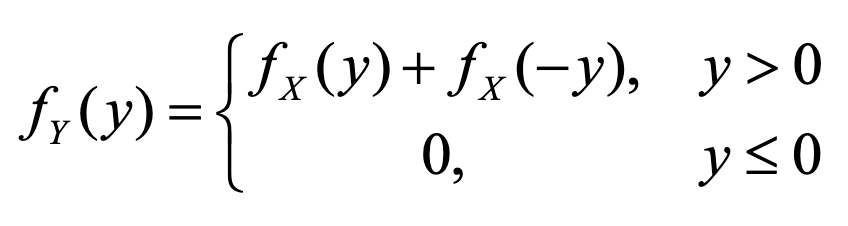
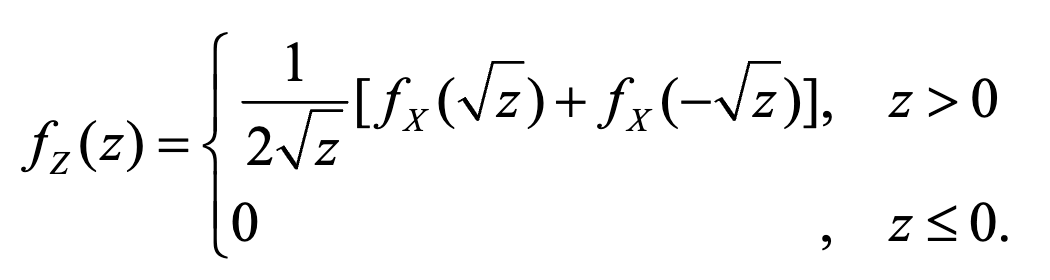
(2)

重要定理:
注意:不单调不能使用定理!题目中如果不单调,要分单调区间进行讨论。
补充
Cov公式
协方差公式为:
其中:
- 和 是两个随机变量。
- 和 是样本中的第 个观测值。
- 和 分别是 和 的样本均值。
- 是样本的数量。
其他的表示方法:(总结)
1. 使用期望表示
协方差的公式可以通过期望来表示:
其中:
- 和 分别是随机变量 和 的期望值。
2. 扩展为两项的差的期望
通过期望的线性性质,可以将协方差展开为以下形式:
此公式表明,协方差等于 和 的乘积的期望减去 和 期望的乘积。
3. 样本协方差形式
在样本数据的情况下,协方差的估计可以表示为:
这里的 是分母,用于样本协方差的无偏估计(即减去自由度)。
4. 矩阵形式
对于多个随机变量 的协方差,可以用协方差矩阵表示,记为 :
协方差矩阵 是一个对称矩阵,其中对角线上的元素为各个变量的方差,非对角线元素为各对变量的协方差。
正态分布变量变形后的性质结论?

