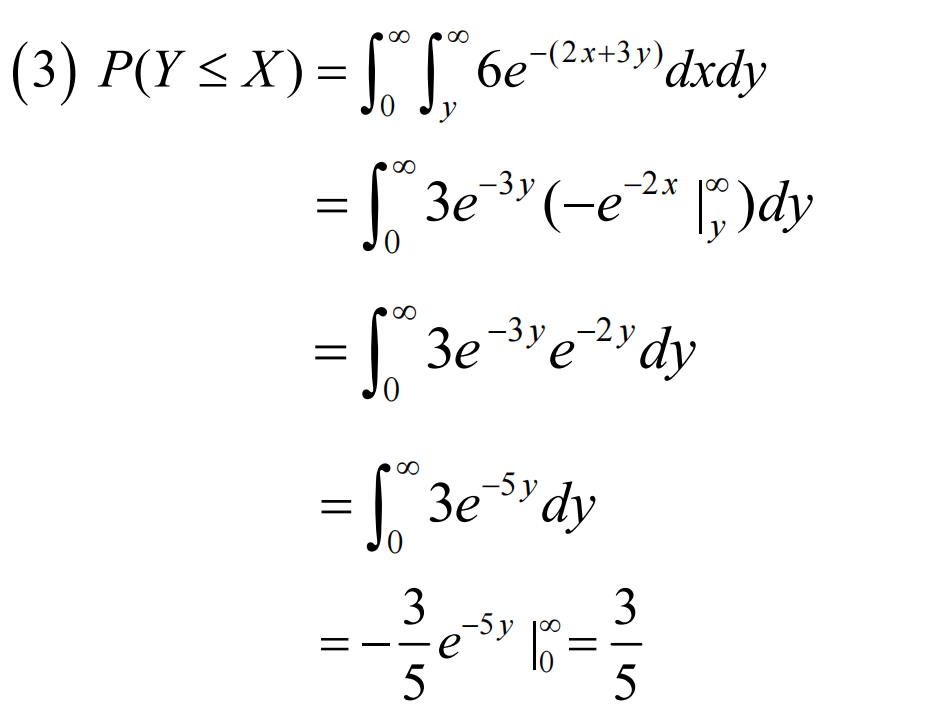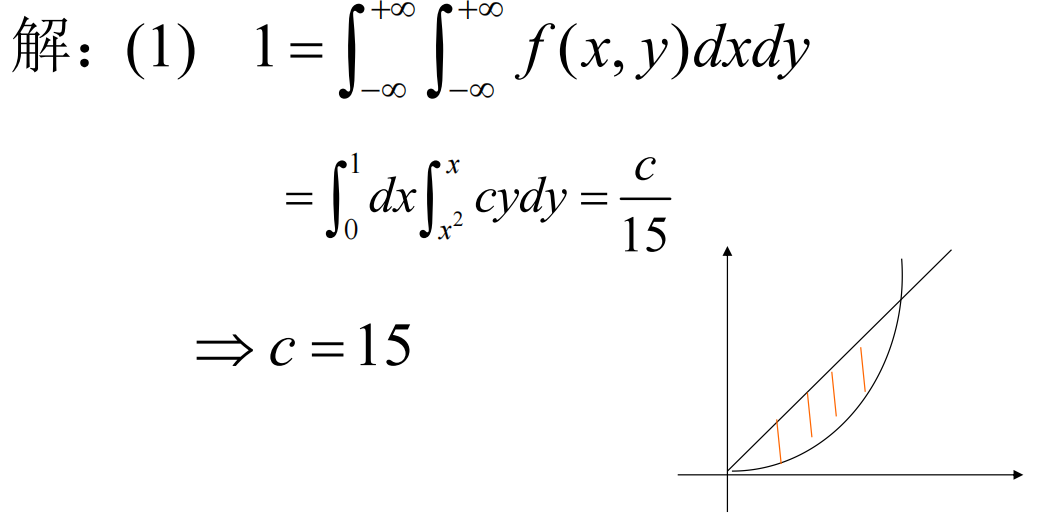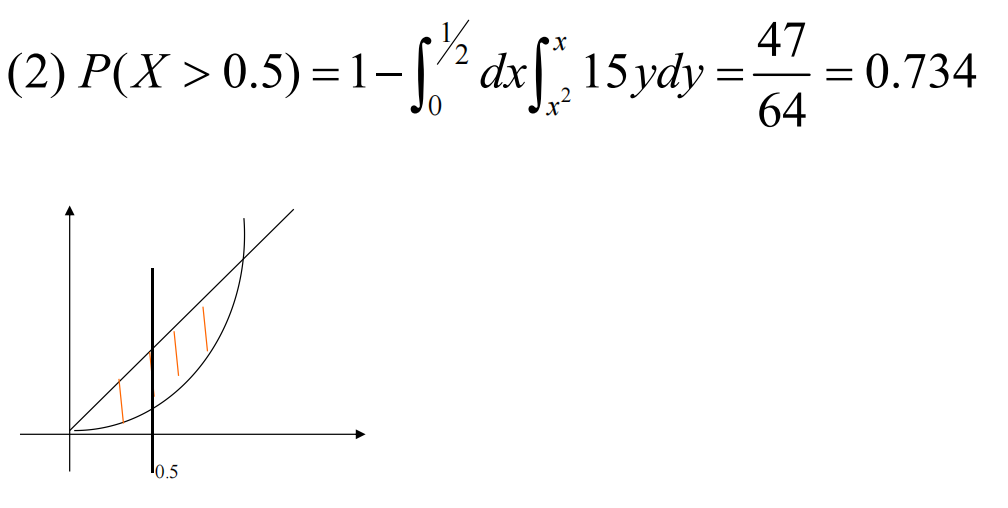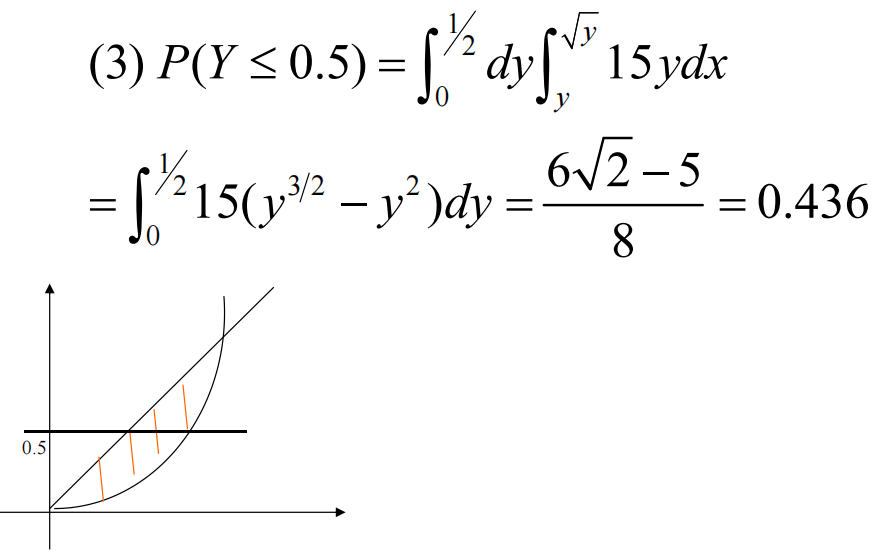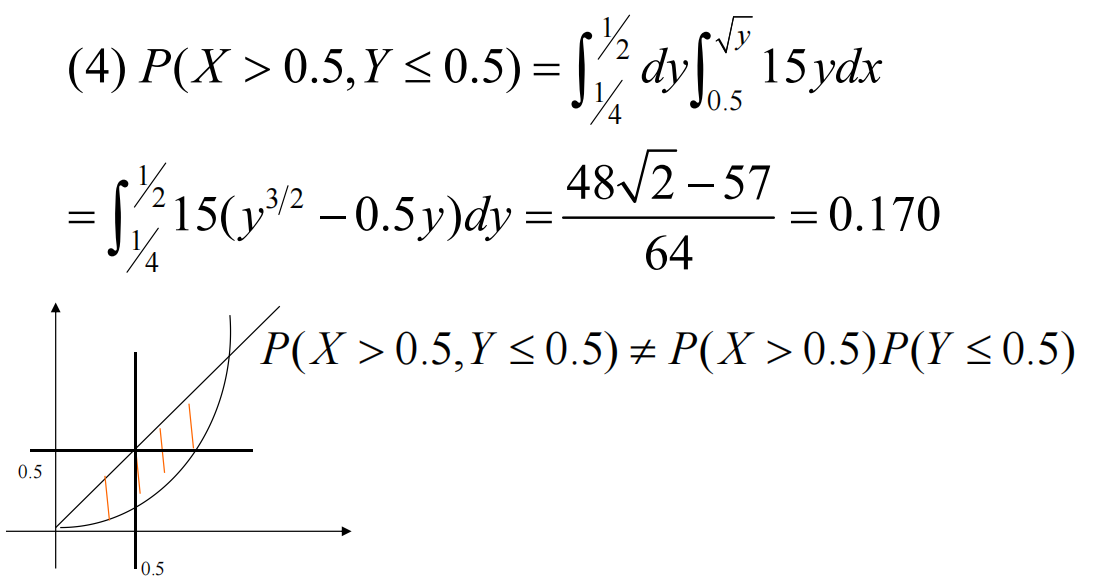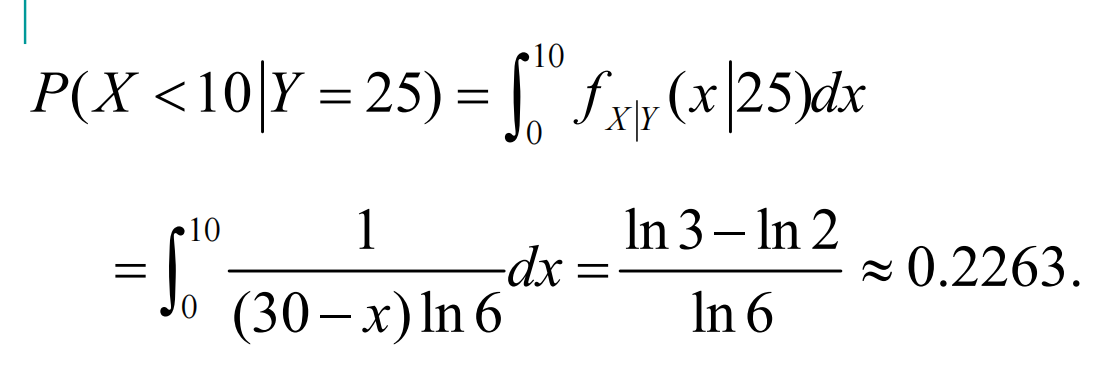1339 字
7 分钟
【概统】第三章整理
目录
二元离散型随机变量
定义
 关注:、都是关于的函数,二元随机变量是指向量
关注:、都是关于的函数,二元随机变量是指向量
联合概率分布
相关概念
- 离散型随机变量:二元随机变量可能取到的不同值是有限对或可列无限对
- 离散型随机变量的联合概率分布律:
联合概率分布律的性质
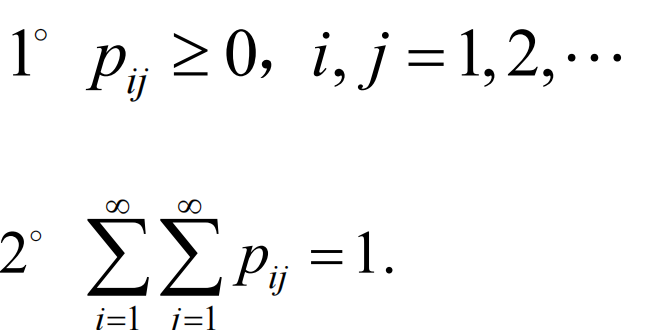 如何描述联合概率分布(题干提问):画表格
如何描述联合概率分布(题干提问):画表格 
边际分布


条件分布

 (解题)如果题干问条件分布律,回答格式:
(解题)如果题干问条件分布律,回答格式:
二元随机变量的分布函数
联合分布函数
1. 定义

2. 性质


边际(边缘)分布函数
 推理:
推理:
条件分布函数

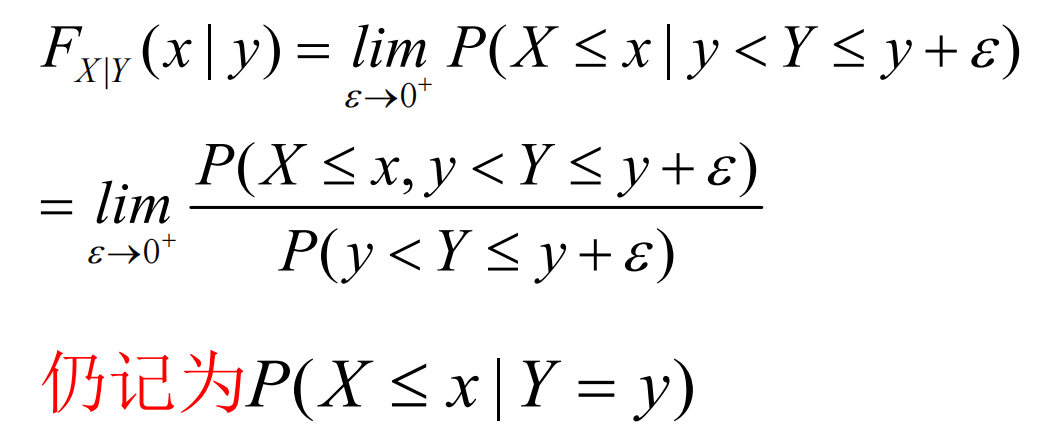
二元连续型随机变量
联合概率密度函数
1. 定义

2. 性质

几何意义:
由于这里是二元变量,所以我通过概率密度函数求解一些事件概率时,通常会看事件代表的平面上几何范围(类似高中线性规划),然后对密度函数在相应的区域上积分,求得事件概率。
- 比如这里的第三问:
- 答案里的积分,本质来源于对y=x曲线上方范围的积分。
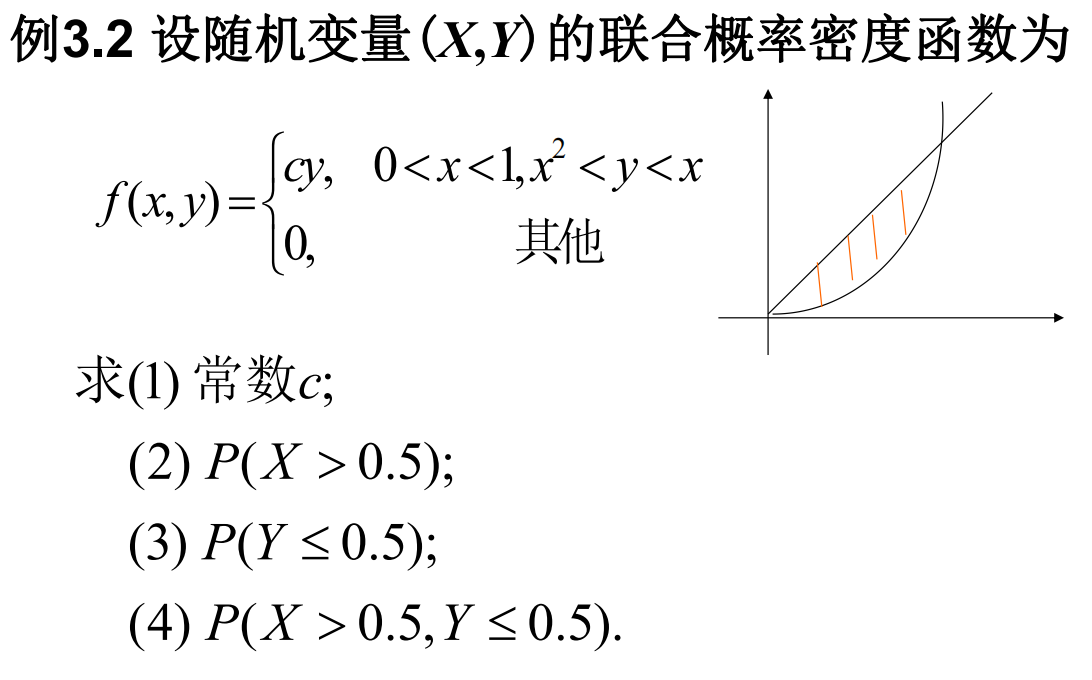
再比如这道题,题干概率密度函数,自变量范围本来就有限制,那么求事件的时候要结合考虑:
边际(边缘)概率密度函数
 和分布函数的关系:
和分布函数的关系: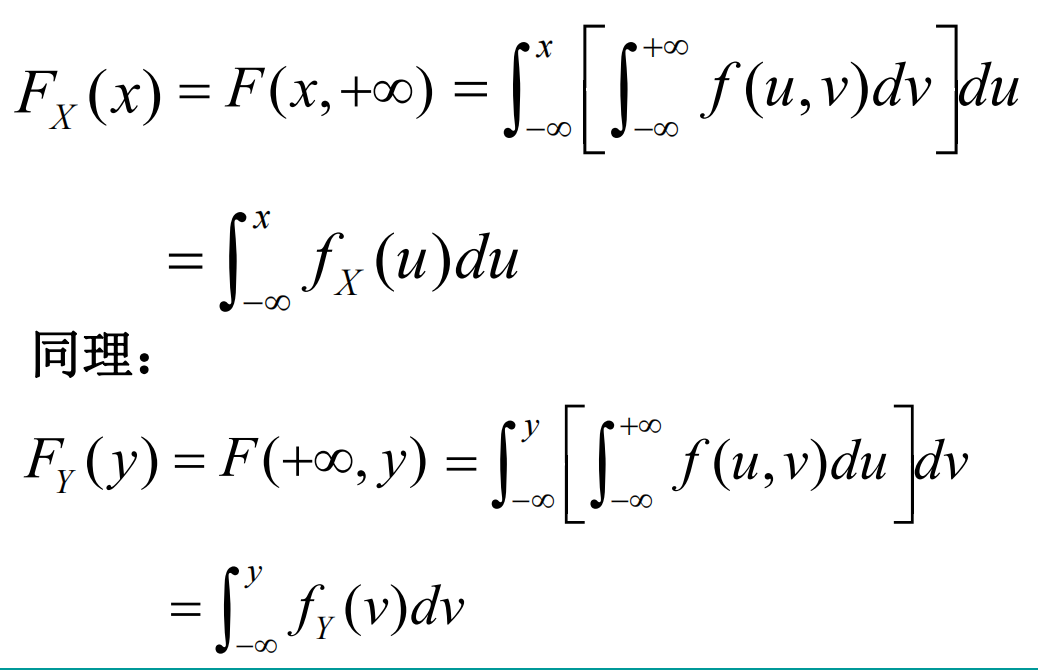
条件概率密度函数
1. 定义
 与概率分布函数的关系:
与概率分布函数的关系: 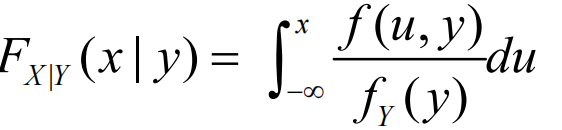
2. 性质
 最后一个结论经常用到,用来求x,y的联合密度函数。
最后一个结论经常用到,用来求x,y的联合密度函数。
一道好题:


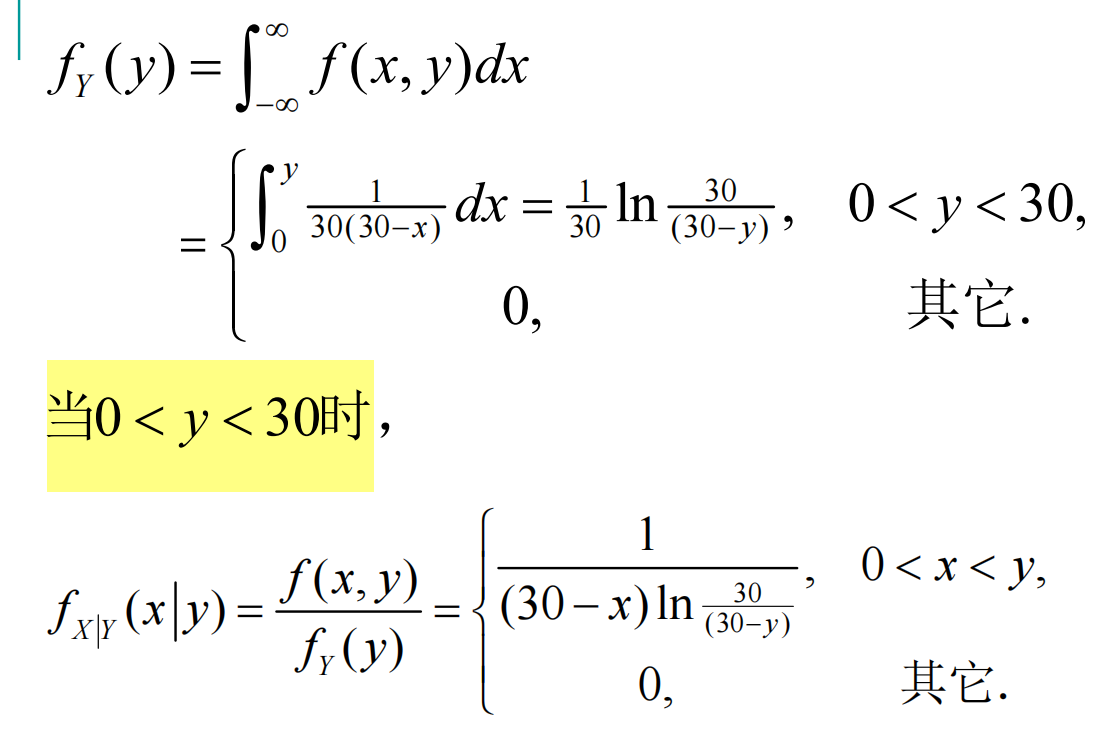
二元均匀分布与二元正态分布
1. 二元均匀分布


- 结论:二元均匀分布的条件分布的条件分布仍为均匀分布
2. 二元正态分布
 其中为的相关系数。
其中为的相关系数。
- 边际密度函数
- X的边际密度函数:

- Y的边际密度函数:
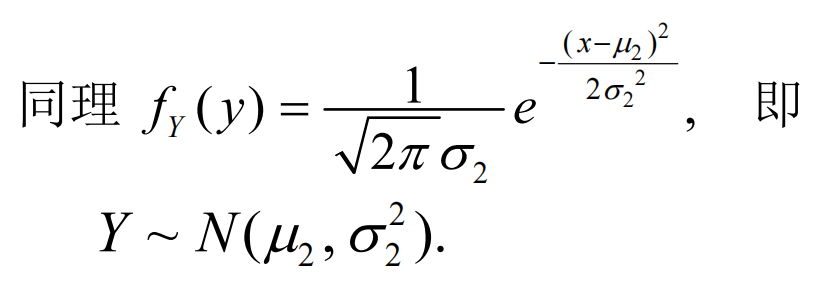
- 可以得出,二元正态分布的边际分布是正态分布,而且不依赖于参数
- X的边际密度函数:
- 条件概率函数
随机变量的独立性
1. 定义
 和离散概率/概率密度的关系:
和离散概率/概率密度的关系:  加上前面定义中的分布函数结论,也经常用来验证X与Y的相互独立性。
加上前面定义中的分布函数结论,也经常用来验证X与Y的相互独立性。
2. 定理:连续型随机变量X,Y相互独立的充要条件
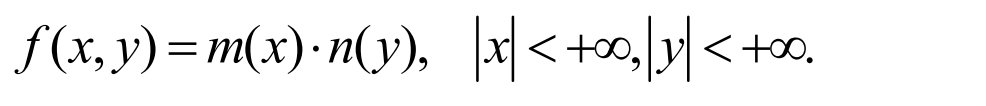
例题:(利用离散型变量相互独立性) 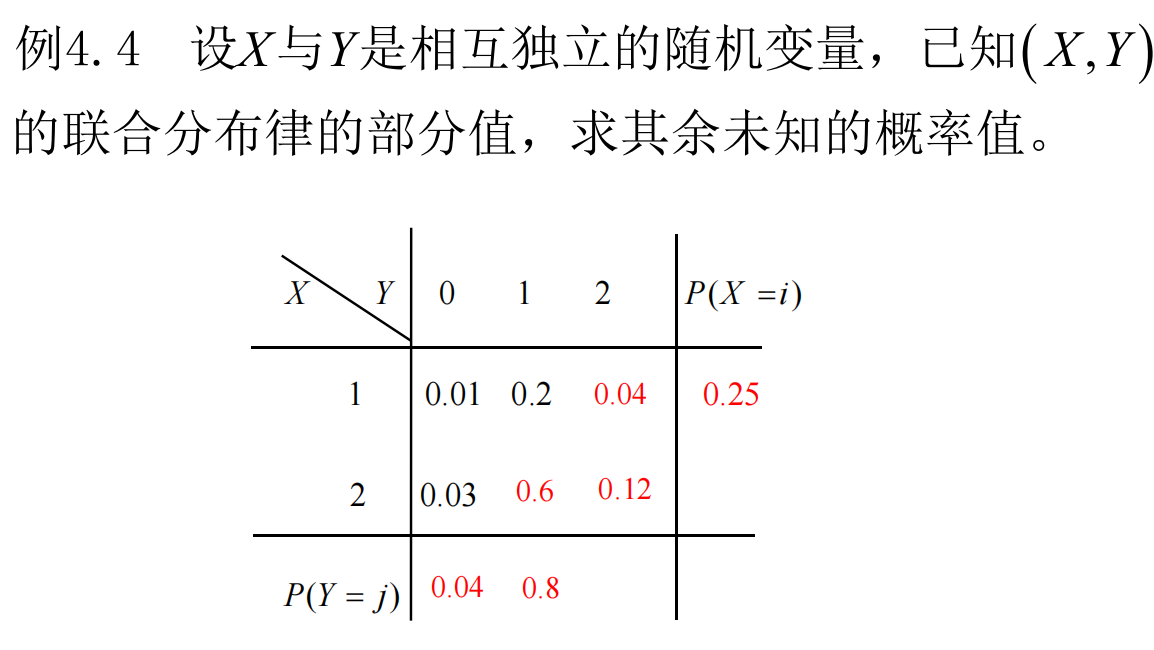 (红色为答案)
(红色为答案)
除此之外,X、Y的相互独立性还可以用来求联合密度函数/边际分布函数
- 结论:对于二维正态随机变量,与相互独立的充要条件是参数
一般n元随机变量的一些概念和结果
1. 定义

2. 分布函数
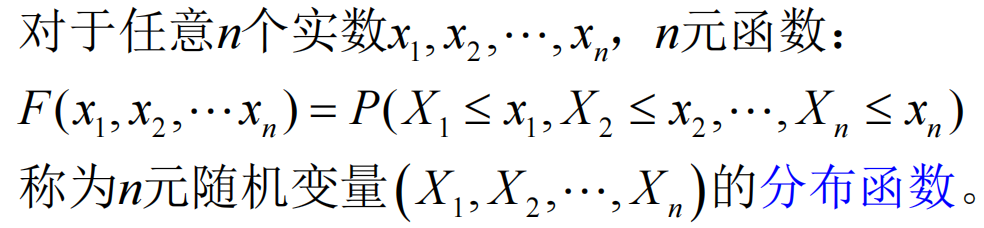
3. 分布律 & 概率密度函数

4. 边际分布

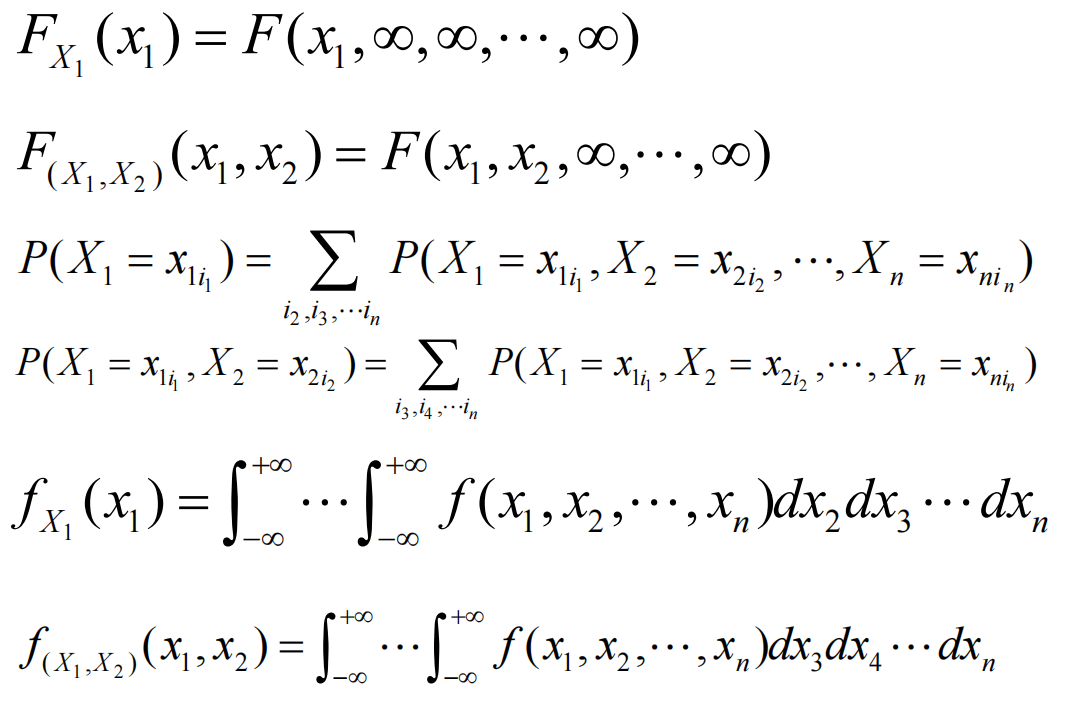
5. 多元随机变量相互独立


定理
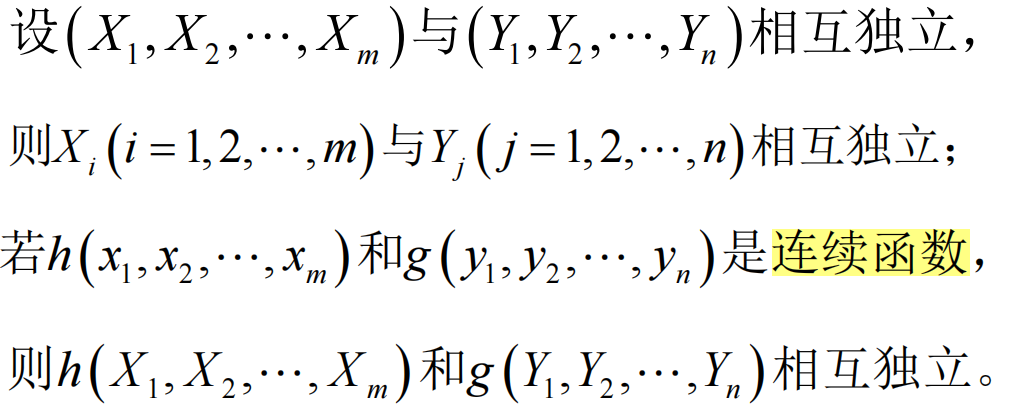
二元随机变量函数的分布
需要了解几种典型的二元随机变量函数分布:
1. Z = X + Y 的分布
分布律
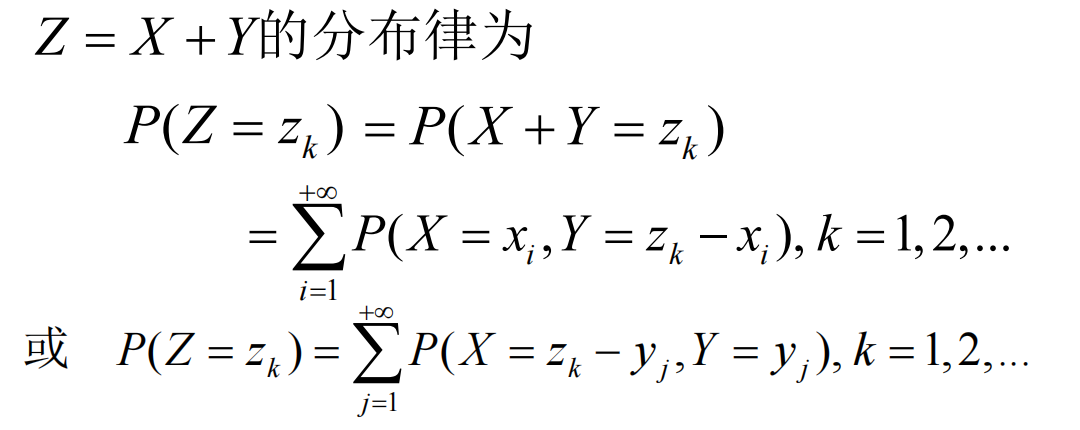
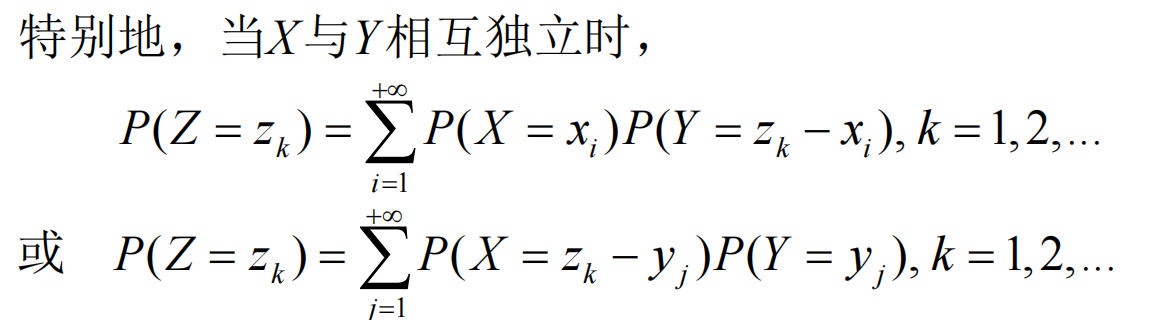
- 结论:泊松分布

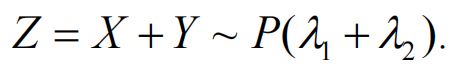
分布函数
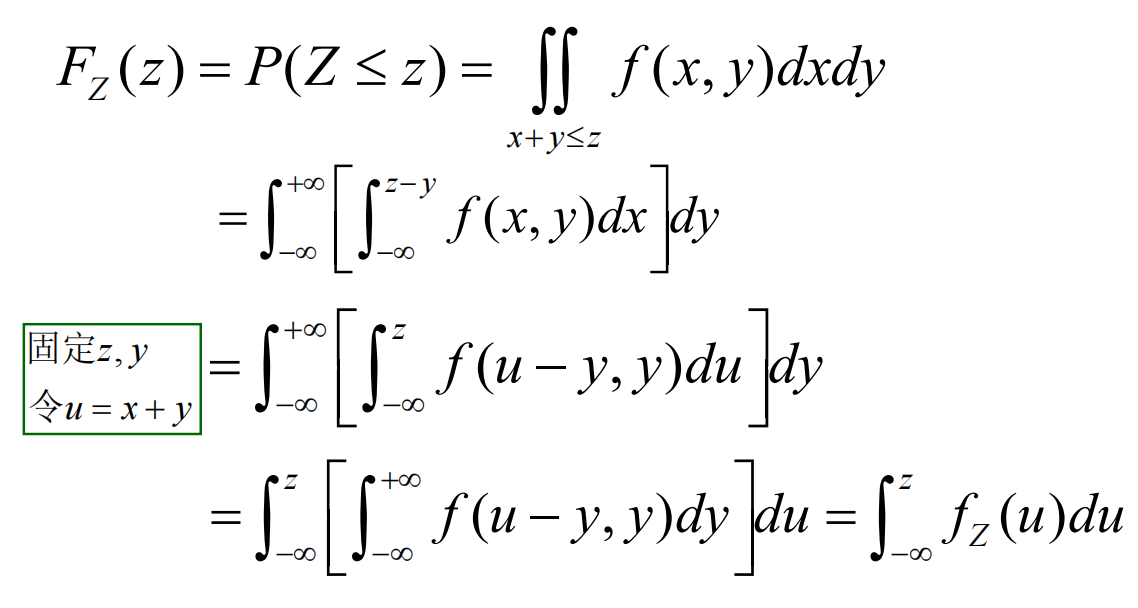
卷积公式
 X与Y独立时非常有用。
X与Y独立时非常有用。
- 结论:相互独立标准正态随机变量X、Y,Z=X+Y的分布:~
- 推广结论:
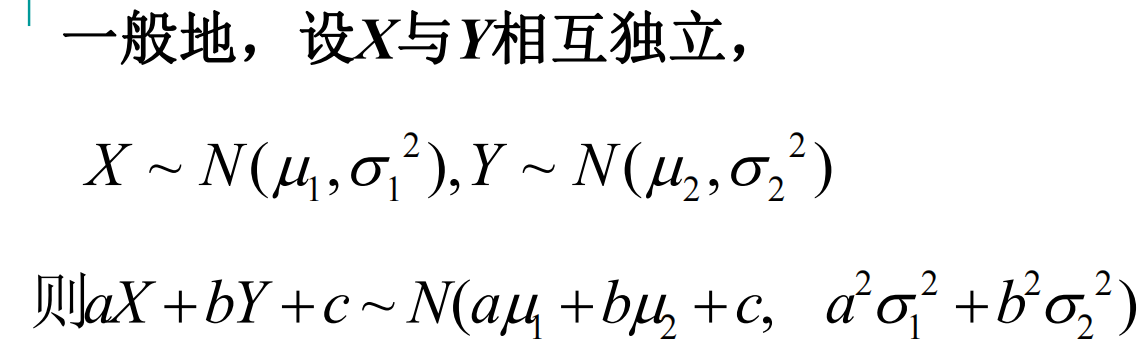
题型:求 Z = X + Y 的概率密度函数
两种方法:
- 利用卷积公式(X,Y独立的情况下)
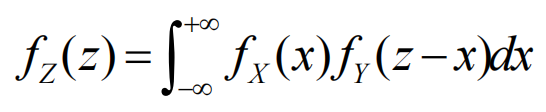 (注意对x,z二元变量范围进行(线性规划)限制)
(注意对x,z二元变量范围进行(线性规划)限制) - 利用分布函数
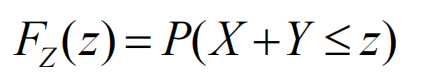 一样(线性规划)找范围,面积求解。
一样(线性规划)找范围,面积求解。
例题: 
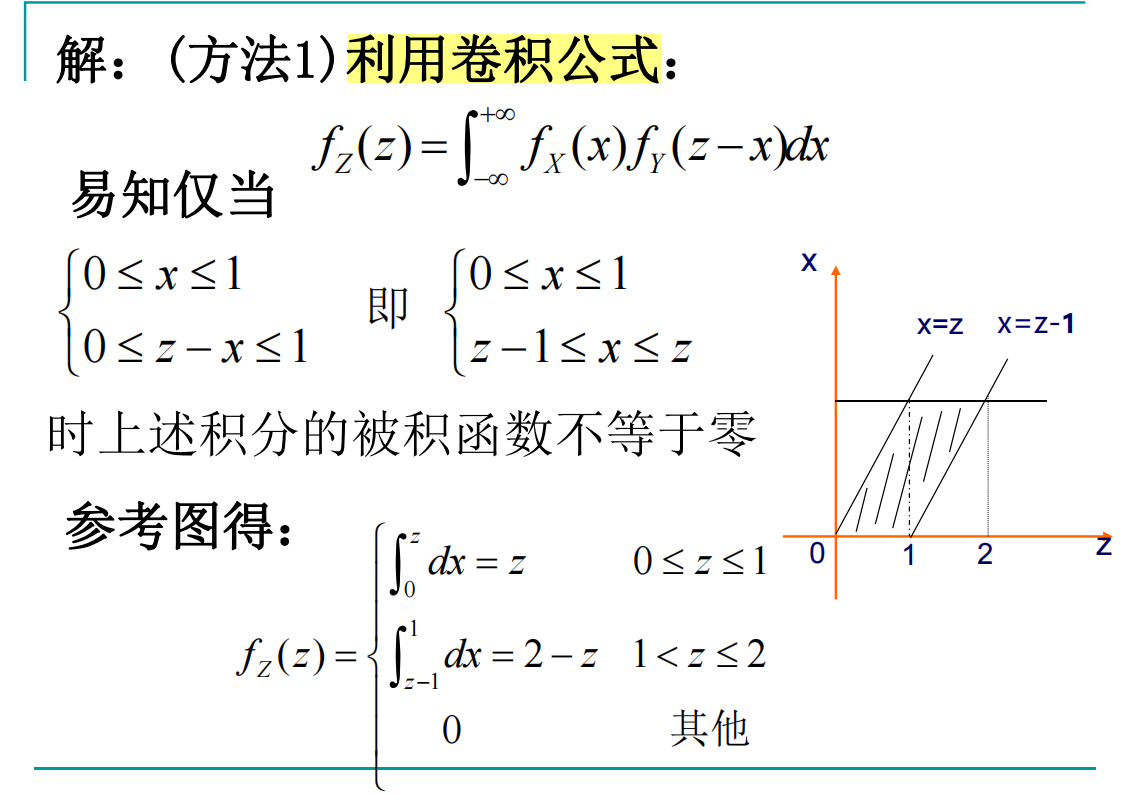
 注意:沿变量轴方向积分
注意:沿变量轴方向积分
如: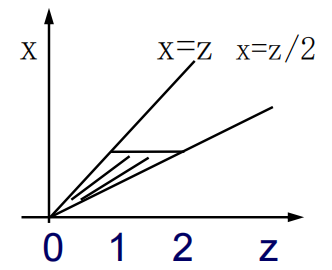 若对x积分: 那么:
若对x积分: 那么: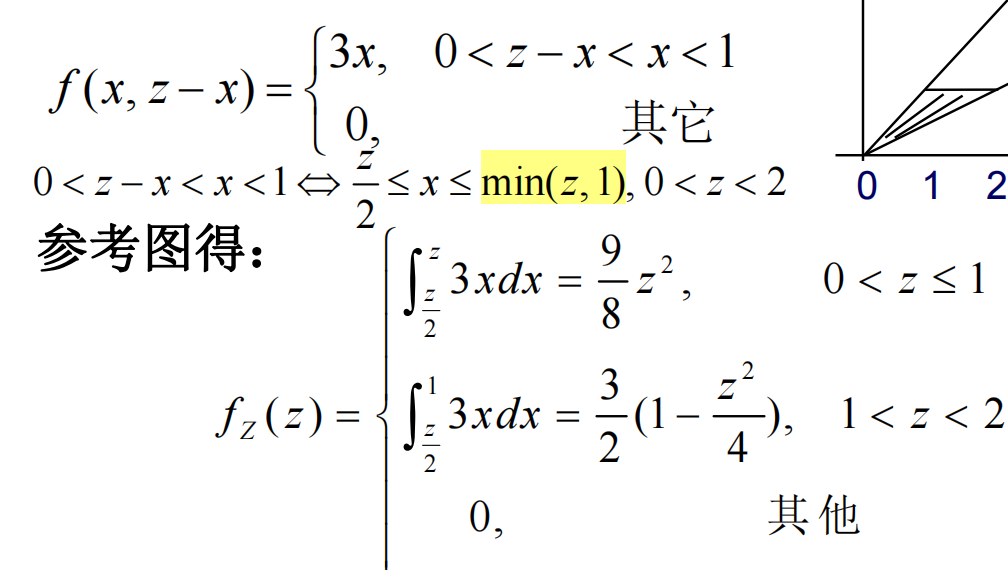
例题: 从分布函数/概率表示事件+全概率公式 来入手,是很常用的方法。
从分布函数/概率表示事件+全概率公式 来入手,是很常用的方法。 
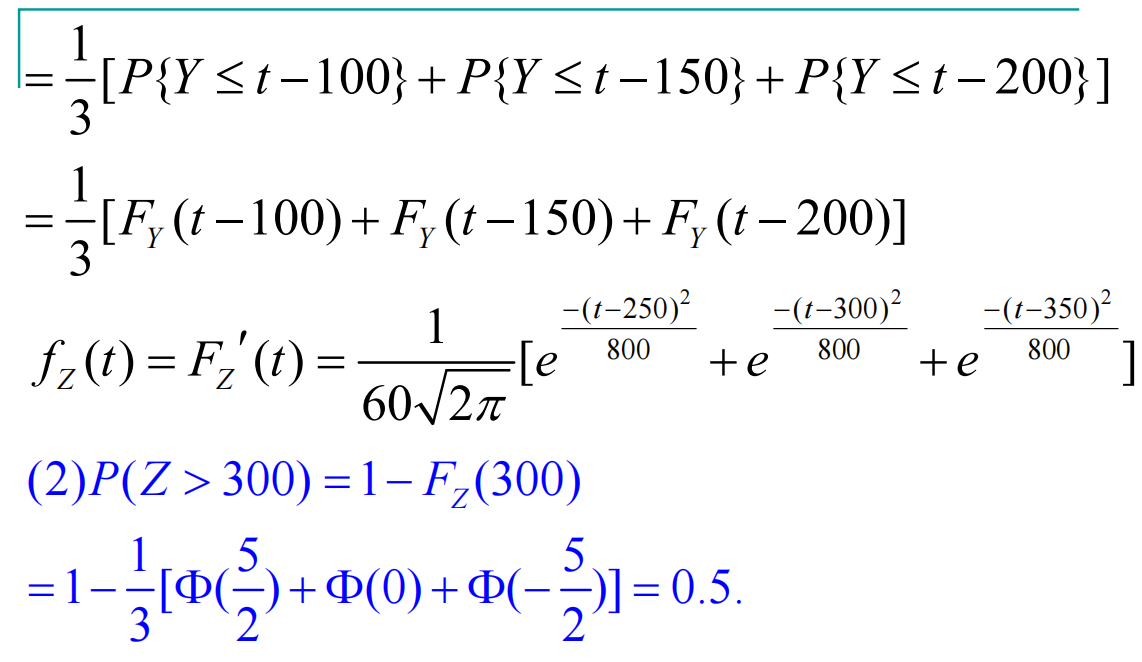 正态分布的分布函数:整体利用和对称思想
正态分布的分布函数:整体利用和对称思想
M = max{X,Y}, N = min{X,Y}的分布

推广到n个相互独立的随机变量的情况

- 常见题型:
- 串并联+备用问题
- 串联:
- 并联:
- 备用: