Content
- MoE(mixture of eXPERTS)
- 异构LLMs / 同构LLMs
- Model Fusion(模型融合)
- diffusion 架构不兼容
- transformer
- RNN
- CNN
- FFN (Feed-forward Network)
- Soft Prompt
- Prediction Heads
- KL Divergence(Kullback-Leibler散度)
- Distance Functions in LLM (Large Language Models)
- Distance Functions in LLM (Large Language Models)
- Cross-Entropy Loss
- Vocabulary in Large Models
- Softmax 操作
- Hidden States
- Attention 注意力机制
- Transformer 模型架构中不同概念的关联
- Transformer 模型架构与公式解析
- 深度学习(Deep Learning)
- Transformer 中的神经网络层构成与分类
- Rouge-L
- 正则化
- Sinkhorn Distance 和 Wasserstein Distance
- Tokenizer
- Logits
- 知识蒸馏(Knowledge Distillation, KD)常见问题与改进方向
- 神经网络中的常见层及其数学原理
- 自回归(Auto-Regressive)属性
- ReLU
- Tokenizer 在 Transformer 模型中的位置
- 交叉熵损失如何监督 Transformer 训练
- Optimal Transport (OT) Matrix(最优传输矩阵)
- dim_feedforward
- Transformer 的前馈神经网络(Feed Forward Network, FFN)
- 低比特量化(Post-Training Quantization)
- LoRA(Low-Rank Adaptation,低秩适应)
- 量化(Quantization)
- 量化过程
- 异常值(Outliers)
- 激活值(Activation)
- DuQuant
MoE(mixture of eXPERTS)
MoE 是 Mixture of Experts 的缩写,中文通常译为“专家混合模型”。这是一个机器学习和深度学习中的模型架构,特别适用于解决大规模和复杂任务。以下是 MoE 的主要概念和特点:
核心思想
MoE 的核心思想是使用多个“专家”模型(或子模型),并根据输入数据的特征,动态地选择和激活最适合的一个或多个专家进行处理。一个“门控机制”(Gate)会负责控制专家的选择,确保不同的输入由最合适的专家处理。
MoE 的组成部分
- 专家网络(Experts)
- 一组子网络,每个网络通常是一个深度神经网络。每个专家专注于特定的数据模式或任务
- 门控网络(Gating Network)
- 负责根据输入生成一个权重向量,表示对每个专家的信任程度。门控网络输出的权重决定了哪些专家会被激活以及各自的参与程度。
- 组合机制
- 根据门控网络的权重,将选中的专家的输出加权求和,生成最终输出。
优点
- 参数规模扩展性
- MoE 使用稀疏激活的方式(只激活部分专家),在增加模型容量的同时有效控制计算成本。
- 任务分解能力
- 每个专家可以专注于学习特定类型的数据模式或任务,提升整体模型的表现力。
- 计算效率
- 虽然模型参数很多,但每次只计算一小部分专家,大幅降低了推理时间。
应用场景
- 自然语言处理(NLP)
- MoE 被广泛用于大规模预训练语言模型(如 Google 的 Switch Transformer 和 GLaM 模型),以提升训练效率和模型性能。
- 计算机视觉(CV)
- 在图像分类、目标检测等任务中,通过 MoE 来处理不同风格或类别的图像。
- 多任务学习
- MoE 可以通过不同专家处理不同任务,方便任务间共享信息。
MoE 的挑战
- 负载均衡问题
- 需要设计好的门控机制,确保专家被均匀使用,避免某些专家过载或长期闲置。
- 训练稳定性
- 动态选择机制可能导致训练不稳定或梯度更新不平衡。
- 稀疏激活优化
- 在稀疏激活时,需要高效实现专家的动态选择和调度。
总结 MoE 是一种高效的模型架构,特别适合参数规模巨大的深度学习任务。通过动态选择专家处理输入,MoE 实现了高性能与计算效率的平衡。
异构LLMs / 同构LLMs
在构建大型语言模型(Large Language Models, LLMs)系统时,异构 LLMs 和 同构 LLMs 是两种不同的架构设计理念。它们的核心区别在于:参与任务的模型是否为相同类型及是否共享参数。
1. 同构 LLMs (Homogeneous LLMs)
定义
- 同构 LLMs 指由多个完全相同或高度相似的模型组成的系统,这些模型具有一致的架构、参数规模或任务能力。
- 特点:
- 共享模型:所有 LLMs 的架构相同,通常使用相同的参数。
- 一致性:模型的行为表现具有一致性,例如生成风格或推理逻辑一致。
应用场景
- 负载均衡:在高并发场景下,为提升响应速度,多个相同的 LLM 实例同时处理不同用户请求。
- 分布式计算:使用多个相同模型协同计算大规模推理任务。
- 流水线优化:模型实例在同一个任务中负责不同的输入批次,但逻辑完全相同。
优点
- 实现简单:由于所有实例相同,管理和训练成本较低。
- 性能一致:不同实例的推理结果在相同条件下是可预测的。
缺点
- 灵活性不足:对于多样化任务场景,模型缺乏针对性优化。
- 资源利用率可能较低:无法根据具体任务调整模型大小或功能。
2. 异构 LLMs (Heterogeneous LLMs)
定义
- 异构 LLMs 指由多个不同的模型组成的系统,这些模型可以具有不同的架构、参数规模、训练目标或专长领域。
- 特点:
- 模型多样性:系统中的 LLMs 可以是大模型、小模型、专用模型等的组合。
- 任务专注性:每个模型在系统中承担特定任务,形成协同效应。
应用场景
- 多模态系统:一个系统中可能包含文本生成模型、图像处理模型和语音识别模型。
- 任务分工:不同模型处理不同类型的任务,例如一个模型负责自然语言生成,另一个负责逻辑推理。
- 边缘计算与云计算结合:小模型用于本地推理,大模型用于云端深度计算。
优点
- 灵活性强:可以针对不同任务定制模型,从而提高性能。
- 资源优化:不同任务可以使用不同大小或架构的模型,避免资源浪费。
- 增强能力:组合多个专用模型可以实现单个模型无法完成的复杂任务。
缺点
- 系统复杂性高:需要设计任务分配、模型协调的机制,增加工程和管理成本。
- 开发成本较高:不同模型可能需要独立训练和优化。
3. 异构 LLMs 和 同构 LLMs 的对比
| 特性 | 同构 LLMs | 异构 LLMs |
|---|---|---|
| 模型架构 | 相同模型架构或实例 | 不同模型架构 |
| 任务分工 | 通常分工不明确或通用化 | 专门分工(如文本生成、逻辑推理等) |
| 灵活性 | 较低 | 较高 |
| 复杂性 | 较低 | 较高 |
| 计算资源利用 | 通常较低 | 较优 |
| 典型应用 | 高并发响应、通用任务处理 | 多模态任务、特定领域任务 |
4. 示例
同构 LLMs
- 一个基于 GPT 的聊天系统同时运行 10 个 GPT-4 实例,用于处理多个用户的对话请求。所有实例模型一致,主要区别在于处理的用户输入不同。
异构 LLMs
- 一个多模态对话系统:
- GPT-4:负责自然语言生成。
- CLIP:负责图像与文本的相关性理解。
- Whisper:负责语音转文本任务。
- 专用逻辑推理模型:用于复杂推理任务。
总结
- 同构 LLMs 适用于通用任务或高并发需求,强调一致性和高效性。
- 异构 LLMs 强调灵活性和任务专注性,适合多样化或复杂任务。
- 系统的选择取决于应用场景的需求以及资源条件。
Model Fusion(模型融合)
模型融合指在机器学习或深度学习中,将多个模型的预测结果进行组合,以提高整体性能或增强模型的鲁棒性。它可以利用不同模型的优势,减少单一模型可能出现的过拟合或偏差,从而获得更好的泛化能力。
模型融合的动机
- 减小误差
- 通过综合多个模型的预测,可以减少单一模型可能存在的偏差或噪声。
- 增强鲁棒性
- 不同模型对数据分布的敏感性不同,融合多个模型可以增强对异常或未知样本的适应能力。
- 利用多样性
- 不同的模型(或同一模型的不同版本)可能在特定区域表现更优,融合可以充分利用这些特性。
模型融合的方法
1. 简单融合
- 直接对多个模型的预测结果进行加权或平均。
方法:
- 平均融合(Averaging):对各模型的预测取平均值。
- 加权融合(Weighted Averaging):为不同模型分配不同权重,根据其性能调整权重大小。
2. 投票法(Voting)
- 适用于分类任务,根据多个模型的预测结果进行多数表决。
方法:
- 硬投票(Hard Voting):选择多数模型预测的类别作为最终结果。
- 软投票(Soft Voting):根据各模型的类别概率分布加权平均,选取概率最大的类别。
3. 堆叠(Stacking)
- 使用另一个模型(元模型)对多个基础模型的预测结果进行学习,从而得到最终预测。
过程:
- 训练多个基础模型(如决策树、SVM、神经网络等)。
- 使用基础模型的预测结果作为新特征,训练一个元模型(如线性回归或更复杂的模型)。
- 元模型输出最终结果。
4. Bagging(自助法,Bootstrap Aggregating)
- 利用不同数据子集训练多个模型,并对其预测结果进行融合。
- 随机森林 是典型的 Bagging 应用。
5. Boosting
- 按序列训练多个模型,每个模型关注前一模型未能正确处理的样本。
- 最终模型通过加权方式融合各阶段模型的结果。
典型方法:
- Adaboost、Gradient Boosting、XGBoost、LightGBM。
6. 模型混合(Ensemble of Ensembles)
- 多层次的融合方法,将上述方法结合使用,进一步提高性能。
模型融合的场景
1. 分类任务
- 在多个分类器之间进行投票或加权平均,减少单个分类器的误差。
2. 回归任务
- 将多个回归模型的输出进行平均或堆叠,提升预测精度。
3. 深度学习中的模型融合
- 在深度学习中,常用以下融合策略:
- 多模型融合:融合多个不同架构的深度学习模型(如 CNN 和 Transformer)。
- 多任务学习:通过共享特征提取层,将多任务模型的预测结果进行融合。
- 多模态数据融合:将来自不同数据源(如图像、文本、音频)的模型融合在一起。
模型融合的优缺点
优点
- 性能提升
- 融合方法通常能提高预测精度,特别是在模型间具有一定多样性的情况下。
- 鲁棒性增强
- 减少单个模型对特定样本或噪声的过度敏感。
- 广泛适用
- 适用于分类、回归、生成任务,以及多模态数据。
缺点
- 计算开销大
- 需要训练多个模型,融合过程可能涉及额外的优化步骤。
- 复杂性提高
- 模型融合引入了新的超参数(如权重分配),优化难度增加。
- 依赖模型多样性
- 如果融合的模型过于相似,可能不会显著提升性能。
应用案例
1. 比赛和排行榜
- 在 Kaggle 等机器学习竞赛中,模型融合几乎是夺冠的必要手段。
- 通常采用 Stacking 或 Voting,结合多个强力模型(如 XGBoost 和深度学习模型)。
2. 生产环境
- 在工业系统中,多个模型融合可以增强系统的鲁棒性,减少对单一模型失效的风险。
3. 深度学习中的应用
- 图像任务:在目标检测、图像分类任务中,融合多个 CNN 模型结果。
- NLP 任务:结合不同语言模型(如 BERT、GPT)的输出以提高文本生成或分类的性能。
总结
模型融合是一种通过集成多个模型提升整体性能的技术方法,具有广泛的应用价值。虽然融合过程增加了计算成本和复杂性,但在性能提升、鲁棒性增强等方面具有明显的优势。
diffusion 架构不兼容
transformer
RNN
CNN
FFN (Feed-forward Network)
Soft Prompt
Prediction Heads
定义
在机器学习和深度学习中,Prediction Heads(预测头)是模型中的组件,通常用来将前面提取到的特征(如通过神经网络提取的特征表示)映射到最终的输出空间。
它们常见于多任务学习、目标检测、自然语言处理等领域,主要功能包括:
- 转换特征到输出:将网络前面提取到的高维特征映射到目标任务的输出(如分类分数、边界框坐标、语言模型的下一个词预测等)。
- 任务专属功能:在多任务学习中,预测头专门针对某一任务(如分类、回归、分割等)做进一步处理。
组成
预测头的组成可能因任务而异,但通常包括以下部分:
- 全连接层(Fully Connected Layers):实现特征到输出的映射。
- 激活函数(如softmax、sigmoid):根据任务需求(分类或回归)进行非线性变换。
- 损失计算模块:有时损失函数也是预测头的一部分,用于指导模型训练。
应用场景
1. 多任务学习
在多任务学习中,模型共享一个主干(backbone)网络提取特征,但使用多个预测头为每个任务提供单独的输出。例如:
- 在图像处理任务中,可能有一个预测头用于分类,另一个用于边界框回归。
2. 目标检测
像 Faster R-CNN 或 YOLO 这样的目标检测模型中,通常包含两个预测头:
- 分类头:输出类别概率。
- 回归头:输出边界框的坐标。
3. 自然语言处理
在语言模型(如BERT、GPT)中:
- 词预测头:预测下一个词或掩盖的词。
- 分类头:在特定任务(如情感分类)中,输出对应类别的概率。
4. Transformer模型
Transformer模型中的预测头通常用于:
- 将Transformer的编码器输出映射到特定任务的目标空间。
- 用于生成或分类等任务。
示例
以BERT为例:
- 主体模型提取文本特征。
- 一个 CLS预测头 将
CLStoken 的特征向量映射到分类任务的类别概率。
以下是使用PyTorch实现的简单预测头代码:
import torch.nn as nn
class PredictionHead(nn.Module):
def __init__(self, input_dim, output_dim):
super(PredictionHead, self).__init__()
self.fc = nn.Linear(input_dim, output_dim)
self.activation = nn.Softmax(dim=-1) # 针对分类任务
def forward(self, x):
x = self.fc(x)
x = self.activation(x)
return x
KL Divergence(Kullback-Leibler散度)
定义
KL散度(Kullback-Leibler Divergence)是一种用于衡量两个概率分布之间差异的非对称度量。
它可以理解为:从分布P到分布Q所需的额外信息量,或者是分布P与分布Q之间的相对熵。
公式如下:
对于连续分布:
其中:
- :真实分布(通常是目标分布)。
- :近似分布(通常是模型预测分布)。
- :以自然对数为底。
性质
非负性:
当且仅当 (P(x) = Q(x)) 对所有 (x) 成立时,(D_{KL}(P || Q) = 0)。
非对称性:
因此,KL散度不是一个严格意义上的距离度量。
对概率分布敏感:
如果 (Q(x)) 在某些点的概率非常低甚至为零,而 (P(x)) 较大,则 KL 散度会趋向无穷大。
直观解释
信息增益:KL散度衡量的是用 近似 时的额外编码开销。
- 如果 和 的分布非常相近,那么 KL 散度会很小。
- 如果 和 差异很大,那么 KL 散度会很大。
模型训练:在机器学习中,KL散度常用于评估模型预测分布 与目标分布 的接近程度。例如:
- 在分类任务中,用KL散度最小化模型预测分布和真实分布之间的差异。
应用场景
概率分布匹配:
- 用于优化生成模型(如变分自编码器,VAE)。
- 衡量预测分布和目标分布的差异。
自然语言处理:
- 比较语言模型生成的概率分布和真实文本分布。
信息论:
- 量化信息增益或相对熵。
强化学习:
- 用于限制策略更新时的分布变化(如TRPO算法)。
示例代码
使用Python计算KL散度:
import numpy as np
from scipy.stats import entropy
# 两个分布
P = np.array([0.4, 0.6]) # 真实分布
Q = np.array([0.5, 0.5]) # 近似分布
# KL散度
kl_divergence = entropy(P, Q)
print(f"KL散度: {kl_divergence}")
Distance Functions in LLM (Large Language Models)
定义
在大语言模型(LLM)中,Distance Functions 是用来度量两个向量、概率分布或嵌入之间差异或相似性的数学工具。
这些函数在模型训练、推理、比较文本表示或优化目标中扮演着重要角色。
常见的距离函数
1. 欧几里得距离(Euclidean Distance)
计算两个向量之间的直线距离,公式为:
- 用途:用于衡量向量的绝对差异。
- 限制:对尺度敏感。
2. 余弦相似度(Cosine Similarity)
衡量两个向量方向的相似性,定义为:
- 范围:。
- 转换为距离:
- 用途:用于文本嵌入表示的相似性比较,尤其当向量的模不重要时。
3. 曼哈顿距离(Manhattan Distance)
计算两个向量之间的绝对差值之和:
- 用途:在高维空间中,适合稀疏向量的距离计算。
4. KL散度(Kullback-Leibler Divergence)
用于衡量两个概率分布之间的差异:
- 用途:衡量模型预测分布和目标分布之间的差异。
- 限制:不对称,即 。
5. Jensen-Shannon散度(Jensen-Shannon Divergence)
KL散度的对称化版本,定义为:
其中 。
- 范围:。
- 用途:用于对称分布比较。
6. Hamming距离(Hamming Distance)
衡量两个向量(或字符串)之间不同位置的数量:
- 用途:主要用于离散数据(如二进制向量)的比较。
7. Wasserstein距离(Earth Mover’s Distance)
用于衡量两个分布之间的最小“搬运成本”:
- 用途:在生成模型(如GAN)中,用于比较生成分布与真实分布。
LLM中的应用
- 嵌入比较:用余弦相似度或欧几里得距离比较文本或词向量的相似性。
- 分布差异:用KL散度或Jensen-Shannon散度评估模型输出概率分布与目标分布的接近程度。
- 模型优化:Wasserstein距离用于优化生成模型(如 Wasserstein GAN)。
示例代码
以下是计算余弦相似度和KL散度的Python代码:
import numpy as np
from scipy.spatial.distance import cosine
from scipy.stats import entropy
# 示例向量
x = np.array([1, 2, 3])
y = np.array([2, 4, 6])
# 余弦相似度
cos_sim = 1 - cosine(x, y)
print(f"余弦相似度: {cos_sim}")
# 概率分布
P = np.array([0.4, 0.6])
Q = np.array([0.5, 0.5])
# KL散度
kl_div = entropy(P, Q)
print(f"KL散度: {kl_div}")
Distance Functions in LLM (Large Language Models)
定义
在大语言模型(LLM)中,Distance Functions 是用来度量两个向量、概率分布或嵌入之间差异或相似性的数学工具。
这些函数在模型训练、推理、比较文本表示或优化目标中扮演着重要角色。
常见的距离函数
1. 欧几里得距离(Euclidean Distance)
计算两个向量之间的直线距离,公式为:
- 用途:用于衡量向量的绝对差异。
- 限制:对尺度敏感。
2. 余弦相似度(Cosine Similarity)
衡量两个向量方向的相似性,定义为:
- 范围:。
- 转换为距离:
- 用途:用于文本嵌入表示的相似性比较,尤其当向量的模不重要时。
3. 曼哈顿距离(Manhattan Distance)
计算两个向量之间的绝对差值之和:
- 用途:在高维空间中,适合稀疏向量的距离计算。
4. KL散度(Kullback-Leibler Divergence)
用于衡量两个概率分布之间的差异:
- 用途:衡量模型预测分布和目标分布之间的差异。
- 限制:不对称,即 。
5. Jensen-Shannon散度(Jensen-Shannon Divergence)
KL散度的对称化版本,定义为:
其中 。
- 范围:。
- 用途:用于对称分布比较。
6. Hamming距离(Hamming Distance)
衡量两个向量(或字符串)之间不同位置的数量:
- 用途:主要用于离散数据(如二进制向量)的比较。
7. Wasserstein距离(Earth Mover’s Distance)
用于衡量两个分布之间的最小“搬运成本”:
- 用途:在生成模型(如GAN)中,用于比较生成分布与真实分布。
LLM中的应用
- 嵌入比较:用余弦相似度或欧几里得距离比较文本或词向量的相似性。
- 分布差异:用KL散度或Jensen-Shannon散度评估模型输出概率分布与目标分布的接近程度。
- 模型优化:Wasserstein距离用于优化生成模型(如 Wasserstein GAN)。
示例代码
以下是计算余弦相似度和KL散度的Python代码:
import numpy as np
from scipy.spatial.distance import cosine
from scipy.stats import entropy
# 示例向量
x = np.array([1, 2, 3])
y = np.array([2, 4, 6])
# 余弦相似度
cos_sim = 1 - cosine(x, y)
print(f"余弦相似度: {cos_sim}")
# 概率分布
P = np.array([0.4, 0.6])
Q = np.array([0.5, 0.5])
# KL散度
kl_div = entropy(P, Q)
print(f"KL散度: {kl_div}")
Cross-Entropy Loss
定义
Cross-Entropy Loss(交叉熵损失)是一种常用的损失函数,特别适用于分类任务。它衡量预测分布与真实分布之间的差异。
在模型训练中,交叉熵损失能够更好地引导模型输出接近目标概率分布。
对于一个样本,其交叉熵损失定义为:
其中:
- :类别总数。
- :真实类别的独热编码(one-hot encoded)值,。
- :模型预测的概率分布,通常是通过 softmax 输出的。
简化公式
对于单个样本,假设真实类别为 ,交叉熵损失可以简化为:
即仅取目标类别的预测概率的对数。
Softmax 和 Cross-Entropy 的关系
交叉熵损失通常与 softmax 函数结合使用:
Softmax 用于将模型的原始输出(logits)转换为概率分布:
其中 是模型对类别 的原始预测值。
Cross-Entropy Loss 对 softmax 输出的概率分布和目标分布进行比较。
应用场景
分类任务:
- 用于多分类问题(如图像分类、文本分类等)。
- 二分类问题是交叉熵损失的特例。
概率分布匹配:
- 衡量模型预测概率分布与真实分布的差异。
特点
- 目标导向:交叉熵惩罚错误预测更大的类别,鼓励模型输出更接近目标类别的概率分布。
- 非负性:交叉熵损失始终为非负值,当预测完全正确时损失为 0。
- 对数缩放:通过取对数,降低了预测置信度过低时的影响。
二分类问题
对于二分类问题(),真实标签 ,交叉熵损失公式可以简化为:
其中 是正类的预测概率。
示例代码
以下是用 Python 计算交叉熵损失的代码:
import numpy as np
# 真实标签(独热编码)
y = np.array([0, 1, 0]) # 类别 2 为真实类别
# 模型预测的概率分布
y_hat = np.array([0.1, 0.7, 0.2])
# 交叉熵损失
loss = -np.sum(y * np.log(y_hat))
print(f"交叉熵损失: {loss}")
Vocabulary in Large Models
定义
在大语言模型(LLM)中,Vocabulary 是指模型能够处理的所有唯一词或子词(tokens)的集合。
模型通过将输入文本分解为这些 tokens,并将其映射为数值表示来处理语言任务。
Vocabulary 的组成
词级别(Word-level Vocabulary):
- 每个单词作为一个 token,例如 “apple” 和 “orange” 是两个不同的词。
- 问题:需要非常大的词表来覆盖所有可能的单词,容易导致稀疏性。
子词级别(Subword-level Vocabulary):
- 将单词拆分为子词(subwords),例如 “unbelievable” 可能分为 “un”, “believ”, 和 “able”。
- 常用算法:
- BPE(Byte Pair Encoding):基于频率合并子词。
- WordPiece:常用于 BERT 等模型,类似于 BPE。
- SentencePiece:适用于任何语言,不依赖空格分割。
字符级别(Character-level Vocabulary):
- 每个字符作为一个 token,例如 “cat” 被分解为 [“c”, “a”, “t”]。
- 问题:虽然能够处理所有语言,但生成较长序列时效率较低。
字节级别(Byte-level Vocabulary):
- 每个字节(byte)作为 token,例如 GPT-2 使用的 Byte Pair Encoding 能很好地处理跨语言文本。
Vocabulary Size 的规定
Vocabulary Size 是指词表中 token 的数量。
- 大小选择的权衡:
- 过大:增加模型复杂度,占用更多内存,训练时间变长。
- 过小:会导致更多的分词,增加序列长度,降低处理效率。
常见模型的 Vocabulary Size
| 模型 | Vocabulary Size | 描述 |
|---|---|---|
| GPT-2 | 50,257 | 使用 Byte-Level BPE。 |
| BERT | 30,000 | 使用 WordPiece。 |
| GPT-3 | ~50,000 | 适配多语言,字节级 BPE。 |
| RoBERTa | 50,265 | 基于 BERT 的改进,扩展词表。 |
决定 Vocabulary Size 的因素
语言特性:
- 单词多变的语言(如英语)需要更大的词表。
- 表意语言(如中文)则需考虑字符或字节级处理。
任务需求:
- 特殊任务(如领域特定词汇)可能需要额外扩展词表。
模型大小:
- 更大的模型可以容纳更大的词表,但对小模型来说,过大的词表会导致稀疏性。
硬件限制:
- 词表越大,需要的内存和计算资源越多。
Vocabulary Size 的优化方法
使用子词分解:
- 通过子词(BPE、WordPiece 等)减少词表大小,同时保持较高的语言覆盖率。
去除低频词:
- 对低频词进行分解,减少无意义的 token。
领域词汇扩展:
- 为领域专属模型添加特定术语。
动态词表(Dynamic Vocabulary):
- 在特定任务中生成适配的词表,而非使用固定词表。
示例:GPT-2 的 Byte-Level BPE
- 输入文本被分割为字节流。
- 常见的字节组合被逐步合并为 tokens。
- 最终形成的词表大小为 50,257,覆盖多语言文本。
Softmax 操作
定义
Softmax 是一种数学函数,常用于将一组任意实数转换为概率分布。
给定一个向量 ,Softmax 的输出是一个长度为 的概率向量,定义为:
其中:
- :指数函数,确保所有值为正数。
- :归一化项,使输出满足概率分布性质,即总和为1。
特性
非负性:Softmax 输出的每一项均为正数。
归一化:Softmax 输出的所有值加起来为1。
指数放大:Softmax 会放大数值差异较大的项,使较大的值占主导地位。
使用场景
分类任务:
- 在多分类问题中,Softmax 用于将模型输出的logits转换为每个类别的概率。
- 结合交叉熵损失(Cross-Entropy Loss)共同使用。
概率建模:
- 用于将分数映射为概率分布,例如语言模型中下一个词的预测。
注意力机制:
- 用于归一化注意力权重,使其表示概率分布。
示例
假设模型的原始输出(logits)为 ,计算 Softmax 输出:
计算指数值:
计算总和:
归一化:
Python 实现
以下是使用NumPy实现Softmax的代码:
import numpy as np
def softmax(z):
expz=np.exp(z-np.max(z)) # 防止数值溢出
return expz/np.sum(expz)
# 示例
logits=np.array([2.0,1.0,0.1])
probs=softmax(logits)
print(probs) # 输出: [0.65900114 0.24243297 0.09856589]
Hidden States
定义
在深度学习模型(尤其是语言模型)中,hidden states 指的是模型在每一层生成的中间特征表示。这些特征是输入通过模型后,在每一层网络中所提取的隐藏状态(hidden states)。
它们反映了模型如何逐步将原始输入转化为更高层次的抽象特征,并在不同层次捕获语义信息。
特性
逐层表示:
- 每一层的 hidden states 是该层网络对输入的特征提取结果,依赖于前一层的输出。
- 例如,对于一个有 层的 Transformer 模型,hidden states 通常表示为:
- :表示输入的初始嵌入(embedding)。
- :表示第 层的隐藏状态。
维度:
- 对于输入序列长度为 ,隐藏层大小为 ,每一层的 hidden states 的维度为:
- 是序列中 token 的数量, 是每个 token 的表示向量维度。
最终输出层:
- 最后一层的 hidden states 通常被用于生成模型的预测结果(如分类概率、生成文本等)。
应用场景
特征提取:
- Hidden states 可以作为中间表示,用于下游任务(如分类、序列标注、情感分析)。
注意力分析:
- 可通过可视化 hidden states,理解模型在不同层如何捕获输入的语义信息。
多层组合:
- 在某些场景下,结合多层 hidden states(而非仅使用最后一层)能提升下游任务的性能。
解释性研究:
- 分析不同层 hidden states 的变化,研究模型学习到的模式。
示例
以下是基于 Hugging Face 的 Transformers 库,提取 BERT 模型的 hidden states 的示例代码:
from transformers import BertModel, BertTokenizer
import torch
# 加载模型和分词器
tokenizer = BertTokenizer.from_pretrained("bert-base-uncased")
model = BertModel.from_pretrained("bert-base-uncased", output_hidden_states=True)
# 输入文本
text = "Hello, how are you?"
inputs = tokenizer(text, return_tensors="pt")
# 前向传播
with torch.no_grad():
outputs = model(**inputs)
# 获取 hidden states
hidden_states = outputs.hidden_states # 一个包含所有层 hidden states 的元组
print(f"Number of layers: {len(hidden_states)}") # 通常包含模型层数 + 1 (embedding层)
print(f"Shape of hidden state for one layer: {hidden_states[-1].shape}") # (batch_size, seq_len, hidden_size)
Attention 注意力机制
定义
注意力机制(Attention Mechanism) 是一种在深度学习模型中模拟人类注意力的机制,能够动态地为输入序列中的不同部分分配权重。它帮助模型关注输入中最重要的信息,同时忽略不相关部分。
Attention 在序列建模任务(如翻译、摘要生成)中尤为重要,能够缓解传统 RNN 和 CNN 对长距离依赖的处理问题。
公式表示
输入与输出
假设输入是一个序列 ,Attention 计算的是:
- 每个输入 与所有其他输入的关系(相关性分数)。
- 使用这些分数加权输入生成输出表示。
Scaled Dot-Product Attention
Attention 的计算公式如下:
相关性分数(Score):
- :查询向量(Query)。
- :键向量(Key)。
归一化(Softmax):
- 是注意力权重,表示每个输入对当前查询的贡献。
- 是缩放因子,用于防止数值过大。
加权求和:
- :值向量(Value)。
- 最终的 Attention 输出是值向量的加权和。
分类
1. 自注意力(Self-Attention)
在自注意力中,查询、键和值都来源于同一序列。
- 应用:Transformer 的核心机制。
2. 交叉注意力(Cross-Attention)
查询、键和值分别来自不同的序列。
- 应用:机器翻译(源语言和目标语言间的注意力)。
3. 多头注意力(Multi-Head Attention)
将注意力分为多个头,分别学习不同的子空间特征:
- 每个头单独计算 Attention。
- 最终将各头的结果拼接并线性变换。
Transformer 中的应用
Transformer 通过多头自注意力完全取代了传统 RNN 的循环结构,实现了高效的全局信息建模。
示例:Transformer 中自注意力的计算流程
- 输入序列 通过线性变换生成 :
- 计算 Attention:
- 多头 Attention 并行执行,结果拼接后通过线性层输出。
示例代码
以下是 Scaled Dot-Product Attention 的实现:
import torch
import torch.nn.functional as F
def scaled_dot_product_attention(query, key, value, mask=None):
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9) # 掩码填充
weights = F.softmax(scores, dim=-1)
return torch.matmul(weights, value)
# 示例输入
q = torch.rand(2, 5, 64) # (batch_size, seq_len, d_k)
k = torch.rand(2, 5, 64)
v = torch.rand(2, 5, 64)
output = scaled_dot_product_attention(q, k, v)
print(output.shape) # 输出形状: (2, 5, 64)
Transformer 模型架构中不同概念的关联
1. Distribution of Probabilities (概率分布)
- 关联部分:输出层(Output Layer)
- 概念描述:
- 概率分布通常出现在 Transformer 模型的最后一层,用于对模型的输出进行归一化(如通过 Softmax 操作)。
- 表示模型对每个可能类别的预测概率。
- 具体实现:
- Transformer 的输出经过线性层后,应用 Softmax,生成分类或下一个 token 的概率分布:
- 是线性变换的输出, 是类别数量或词汇表大小。
- 概念描述:
2. Representation Space (表示空间)
- 关联部分:每一层的输出特征(特别是最后一层隐藏状态)
- 概念描述:
- 表示空间是 Transformer 模型中通过编码器或解码器层提取的高维向量空间。
- 不同 token 或句子在这个空间中被表示为向量,其分布可以反映语义相似性。
- 具体实现:
- 词级表示:Transformer 层的每个 token 输出的向量都属于表示空间。
- 句级表示:对词级表示进行池化(如平均或最大池化)得到句子级别的表示。
- 概念描述:
3. Hidden States (隐藏状态)
- 关联部分:每一层的中间输出
- 概念描述:
- Hidden States 是 Transformer 中间层的输出,表示输入数据在该层的特征表示。
- 包括输入嵌入(embedding)和每一层经过自注意力和前馈神经网络的处理结果。
- 具体实现:
- 对于一个具有 层的 Transformer 模型,hidden states 通常表示为:
- 是输入的嵌入表示。
- 是第 层的输出。
- 对于一个具有 层的 Transformer 模型,hidden states 通常表示为:
- 概念描述:
总结表格
| 概念 | 关联部分 | 作用 |
|---|---|---|
| Distribution of Probabilities | 输出层(Softmax 归一化) | 提供对每个类别(或下一个 token)的预测概率,用于分类或生成。 |
| Representation Space | 每一层(特别是最后一层的输出) | 表示输入数据的特征向量空间,用于捕获词语或句子的语义特征。 |
| Hidden States | 所有层的中间输出 | 逐层提取的特征表示,包含从低级特征到高级语义信息,用于多任务或多层级特征分析。 |
Transformer 模型架构与公式解析
私链🔗:
Transformer 模型是由 Vaswani 等人于 2017 年提出的,它通过完全基于注意力机制(Attention Mechanism)来处理序列数据,尤其在自然语言处理(NLP)任务中取得了巨大的成功。与传统的 RNN 和 LSTM 模型不同,Transformer 使用自注意力(Self-Attention)和位置编码(Positional Encoding)来建模序列的长期依赖。
Transformer 模型架构
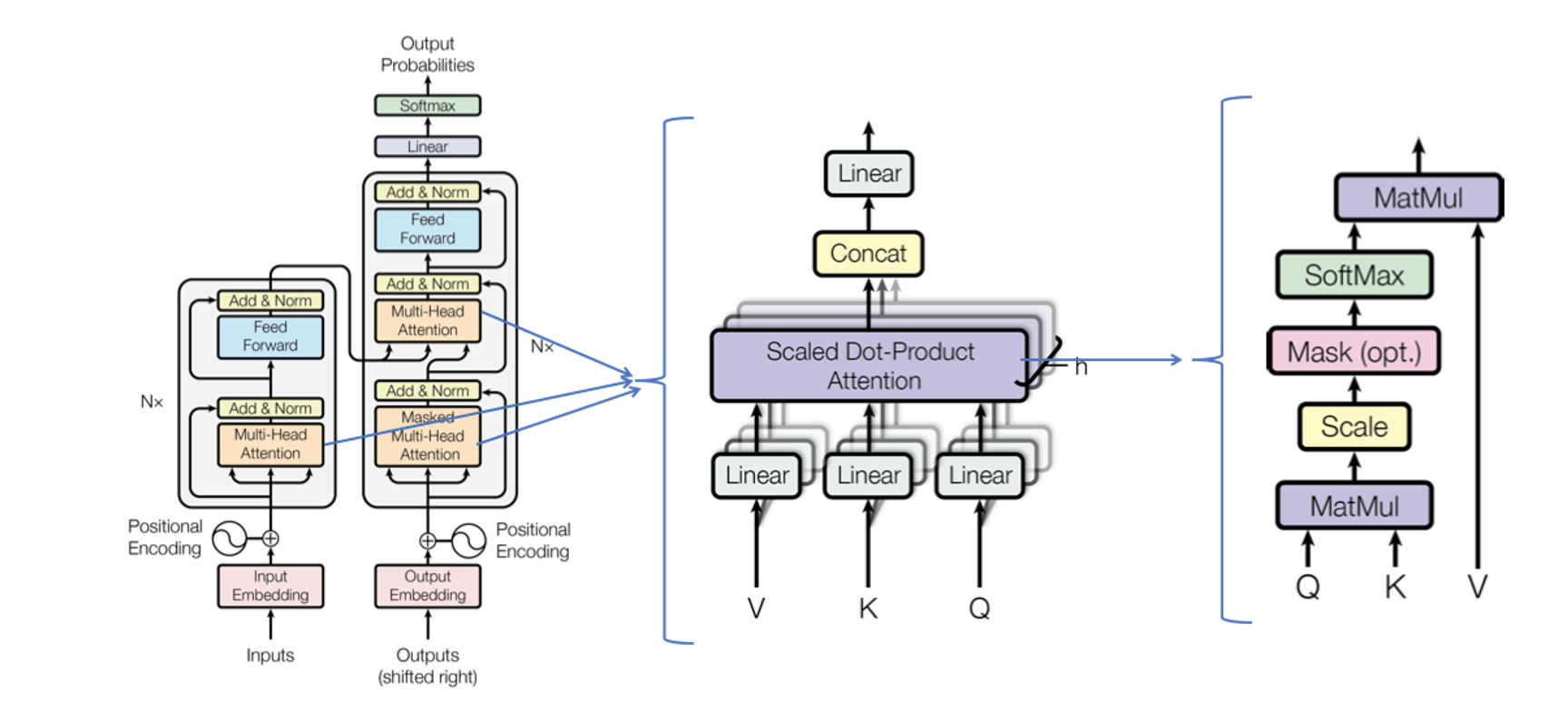 Transformer 的架构由两个主要部分组成:
Transformer 的架构由两个主要部分组成:
- 编码器(Encoder):将输入序列映射到隐藏表示。
- 解码器(Decoder):生成目标序列,通常用于序列到序列的任务(如机器翻译)。
编码器(Encoder)
- 编码器由 层堆叠的相同模块组成,每个模块包括两个子层:
- 多头自注意力(Multi-Head Self-Attention)
- 前馈神经网络(Feed Forward Neural Network)
1. 多头自注意力(Multi-Head Self-Attention)
- 目的:自注意力机制允许模型在处理当前单词时关注到输入序列中的其他所有单词,从而捕捉全局信息。
- 公式:
查询、键、值(Query, Key, Value): 其中 是输入(通常是词嵌入或前一层的输出),, , 是权重矩阵。
计算注意力分数(Scaled Dot-Product Attention):
- 这里, 是查询和键的维度,用于缩放避免过大的数值。
应用 Softmax 和加权求和:
多头注意力:
- 每个头的计算独立进行,然后拼接并通过线性变换 。
2. 前馈神经网络(Feed Forward Neural Network)
- 作用:每个位置的输出都通过一个两层的前馈神经网络,通常包括 ReLU 激活函数。
- 公式:
解码器(Decoder)
解码器的结构与编码器类似,但它有三个子层:
- 多头自注意力(Masked Self-Attention):解码器只关注当前位置及之前的输出(masked)。
- 编码-解码注意力(Encoder-Decoder Attention):这一步通过编码器的输出和解码器的输入计算注意力,帮助生成与输入相关的输出。
- 前馈神经网络(Feed Forward Neural Network):与编码器相同。
解码器中注意力的变更
Masked Self-Attention: 在解码器中,为了确保生成的 token 只能依赖于之前的 token(而不是未来的 token),需要对 self-attention 进行掩码处理:
Encoder-Decoder Attention: 在解码器的第二个子层,查询来自解码器输入,键和值来自编码器输出。通过这种方式,解码器能够关注编码器提取的输入信息。
位置编码(Positional Encoding)
由于 Transformer 完全依赖于注意力机制而没有递归结构,因此需要额外的 位置编码 来为模型提供序列中词语的顺序信息。位置编码是与输入嵌入相加的:
- 其中, 是词语的位置信息, 是维度索引, 是嵌入维度。
Transformer 模型的完整流程
输入嵌入(Input Embedding): 输入序列被映射到一个稠密的向量空间,并与位置编码相加。
编码器: 编码器的每一层通过多头自注意力和前馈神经网络处理输入序列,生成序列的高维表示。
解码器: 解码器使用编码器的输出和目标序列的部分信息生成目标序列的下一部分。
输出层: 最后的解码器输出经过线性变换和 softmax 操作,生成目标序列中每个词汇的概率分布。
Transformer 模型的优缺点
优点
- 并行化:Transformer 模型不像 RNN,能够并行处理整个输入序列,显著提高了训练效率。
- 长距离依赖:通过自注意力机制,Transformer 可以捕捉序列中的长距离依赖关系。
缺点
- 计算复杂度:自注意力机制的时间复杂度为 ,在处理非常长的序列时计算开销较大。
- 内存消耗:需要存储大量的中间结果,尤其是在多头注意力机制和大规模训练时。
总结
Transformer 模型通过自注意力和前馈神经网络结构有效地处理了序列数据,尤其在 NLP 任务中得到了广泛应用。模型的关键在于注意力机制,它使得每个输入位置可以动态地关注到序列中其他位置的信息。通过堆叠多个编码器和解码器层,Transformer 实现了强大的建模能力。
深度学习(Deep Learning)
定义
深度学习是机器学习的一个分支,其核心思想是通过多层神经网络来模拟人脑的学习过程,从数据中自动提取特征并进行决策或生成。它是一种以**人工神经网络(Artificial Neural Networks, ANN)**为基础的技术,通常包含多个隐藏层(即“深度”)。
核心概念
1. 神经网络(Neural Networks)
- 深度学习模型由神经网络构成,每个网络由输入层、隐藏层和输出层组成。
- 神经网络的基本单元是“神经元”,其计算如下:
- :输入特征。
- :权重。
- :偏置。
- :激活函数,用于引入非线性。
2. 深度(Depth)
- 深度指的是神经网络中的层数,深度学习模型通常包含多层隐藏层,相比于传统的浅层模型,能够提取更复杂的特征。
3. 特征自动提取
- 深度学习不需要手工设计特征,而是通过模型的训练自动学习特征表示。
4. 监督与非监督学习
- 监督学习:使用标注数据进行训练,例如图像分类、语音识别。
- 非监督学习:使用无标签数据进行模式发现,例如聚类、生成模型。
工作流程
数据准备:
- 收集并预处理数据(例如归一化、去噪)。
- 通常需要大量的数据以避免过拟合。
模型设计:
- 选择适当的神经网络架构(如卷积神经网络、循环神经网络、Transformer 等)。
- 定义输入和输出的维度。
模型训练:
- 利用反向传播算法(Backpropagation)和梯度下降优化权重。
- 通过损失函数(如交叉熵、均方误差)评估模型性能:
模型评估:
- 使用验证集检查模型的泛化性能。
- 通过指标(如准确率、精确率、召回率、F1 分数)评估效果。
模型部署:
- 将训练好的模型部署到生产环境中,进行预测或生成任务。
常见架构
1. 全连接网络(Fully Connected Networks, FCN)
- 每个神经元与上一层的所有神经元相连。
- 应用场景:表格数据、基础分类任务。
2. 卷积神经网络(Convolutional Neural Networks, CNNs)
- 利用卷积操作提取局部特征,适用于处理图像数据。
- 结构包括卷积层、池化层和全连接层。
3. 循环神经网络(Recurrent Neural Networks, RNNs)
- 适用于序列数据(如时间序列、文本)。
- 变种包括 LSTM 和 GRU,用于解决长程依赖问题。
4. Transformer
- 基于注意力机制,能够处理长序列。
- 应用场景:自然语言处理、图像生成。
5. 生成对抗网络(Generative Adversarial Networks, GANs)
- 包含生成器和判别器,用于生成数据(如图像生成、文本生成)。
深度学习的优缺点
优点
- 高性能:在大规模数据和计算资源下,深度学习模型表现出色。
- 自动化特征提取:无需手工设计特征。
- 广泛应用:适用于图像、语音、自然语言处理等多个领域。
缺点
- 计算成本高:需要强大的计算资源(如 GPU)。
- 数据需求大:模型训练通常需要大量标注数据。
- 可解释性差:模型内部的权重和结构通常很难直接解释。
应用领域
- 计算机视觉(CV):
- 图像分类、目标检测、图像分割。
- 自然语言处理(NLP):
- 机器翻译、文本生成、问答系统。
- 语音识别:
- 语音转文本、语音合成。
- 自动驾驶:
- 环境感知、路径规划。
- 医疗诊断:
- 图像分析、疾病预测。
总结
深度学习是人工智能的重要分支,通过多层神经网络从数据中学习特征表示,能够在多种复杂任务中实现高性能。随着计算资源的增强和模型架构的优化,深度学习的应用场景不断扩大,其潜力也在逐步释放。
Transformer 中的神经网络层构成与分类
Transformer 是一种基于注意力机制的深度学习模型,其神经网络层可以分为两大主要部分:编码器(Encoder) 和 解码器(Decoder)。每个部分由多个重复堆叠的层(Layer)组成,而每层又由特定功能的子结构模块构成。
1. Transformer 的基础组成
每层结构
Transformer 的编码器和解码器层都包含以下基本模块:
1.1 多头注意力机制(Multi-Head Attention)
- 核心功能:通过自注意力(Self-Attention)或交互注意力(Cross-Attention)机制,使模型能够从输入序列中提取全局依赖关系。
- 组成:
- 输入:查询(Query, )、键(Key, )、值(Value, )。
- 运算:基于注意力机制:
- 多头机制:将注意力机制并行化: 每个头有独立的参数 。
1.2 前馈神经网络(Feed Forward Neural Network, FFN)
- 核心功能:对每个位置单独作用的两层全连接网络,用于非线性特征变换。
- 公式:
- 是权重矩阵, 是偏置。
1.3 残差连接和层归一化(Residual Connection & Layer Normalization)
- 核心功能:
- 残差连接:跳跃连接输入和输出以缓解梯度消失问题:
- 层归一化:对每层输入进行归一化,稳定训练过程。
1.4 位置编码(Positional Encoding, PE)
- 核心功能:弥补 Transformer 无法捕捉序列顺序信息的缺陷。
- 公式: 对于位置 和嵌入维度 : 实现:通过将位置编码与输入嵌入直接相加。
2. 分类与详细结构
2.1 编码器(Encoder)层
功能:将输入序列编码为隐藏表示。
组成模块:
- 多头自注意力机制(Self-Attention)。
- 前馈神经网络(FFN)。
- 残差连接和层归一化。
特点:
- 每个位置的表示可以关注输入序列的所有位置。
- 结构对称,层与层之间无差别。
2.2 解码器(Decoder)层
功能:生成目标序列,每一步依赖于之前的输出和编码器的隐藏表示。
组成模块:
- Masked 多头自注意力:
- 掩码机制(Masking)确保解码器的生成只关注当前位置及之前的位置。
- 编码器-解码器注意力(Encoder-Decoder Attention):
- 查询来自解码器输入,键和值来自编码器输出,用于对输入序列进行交互建模。
- 前馈神经网络(FFN)。
- 残差连接和层归一化。
- Masked 多头自注意力:
特点:
- 解码器的自注意力是“因果性”的,确保输出的生成顺序正确。
- 增加了与编码器交互的注意力模块。
3. 分类总结
| 模块类别 | 功能 | 公式或机制 |
|---|---|---|
| 注意力机制 | 捕捉序列间的全局依赖关系,分为自注意力和交互注意力。 | 计算注意力分布,Softmax 归一化后加权求和值。 |
| 前馈神经网络 | 非线性特征变换,提高模型表达能力。 | 两层线性变换: |
| 残差连接和归一化 | 加速收敛,稳定训练过程,避免梯度消失。 | |
| 位置编码 | 为序列数据提供位置信息。 | 和 函数提供不同频率的信息。 |
4. 整体架构流程
编码器:
- 输入嵌入与位置编码相加。
- 多头自注意力计算序列间的全局依赖。
- 前馈神经网络进行特征变换。
- 残差连接和归一化后输出。
解码器:
- 输入嵌入与位置编码相加。
- Masked 多头自注意力生成序列。
- 编码器-解码器注意力引入输入序列信息。
- 前馈神经网络特征变换。
- 残差连接和归一化后输出。
通过上述模块的堆叠和交互,Transformer 模型能够高效捕捉序列数据中的复杂关系。
Rouge-L
Rouge-L 是一种用于评估文本摘要质量的指标,它衡量生成摘要与参考摘要之间 n-gram 的匹配程度。其中,n-gram 指的是包含 n 个单词的连续片段。Rouge-L 通常使用最长公共子序列 (Longest Common Subsequence, LCS) 来计算 n-gram 的匹配程度
正则化
正则化(Regularization) 是在机器学习和深度学习中用于防止模型过拟合(Overfitting)的一种技术。它的核心思想是在损失函数中添加一个惩罚项,限制模型的复杂度,从而提高模型对未见数据(测试集)的泛化能力。
为什么需要正则化?
在机器学习中,我们的目标是训练一个能很好地泛化(generalize)的模型,即在训练集上表现良好的同时,在测试集上也能表现良好。然而,如果模型过于复杂(比如过多的参数、过高的自由度),它可能会“记住”训练数据中的噪声,而不是学习数据的真正模式,从而导致过拟合。
正则化的作用就是减少模型的复杂度,防止它过度拟合训练数据,以提高泛化能力。
常见的正则化方法
1. L1 正则化(Lasso)
L1 正则化 通过在损失函数中添加参数的 L1 范数(绝对值和) 作为惩罚项,使某些权重变为0,从而达到特征选择的效果。
- 效果:L1 正则化会让某些权重变成 0,因此它可以用于特征选择(Feature Selection)。
- 常见应用:Lasso 回归(L1 正则化的线性回归)。
- 缺点:当特征高度相关时,L1 可能会随机选择某些特征,而不是均匀分配权重。
2. L2 正则化(Ridge)
L2 正则化 通过在损失函数中添加参数的 L2 范数(平方和) 作为惩罚项,使权重趋向于较小的值(接近但不等于0)。
- 效果:L2 正则化会让所有权重变小,而不会完全变成 0。
- 常见应用:Ridge 回归(L2 正则化的线性回归),深度学习中的权重衰减(Weight Decay)。
- 优点:在特征相关性较高时,L2 比 L1 更稳定。
3. Elastic Net
Elastic Net 结合了 L1 和 L2 正则化:
- 效果:既能稀疏化权重(L1),又能防止特征相关性问题(L2)。
- 常见应用:当数据有很多特征,并且特征之间有较高相关性时,Elastic Net 是一个好的选择。
4. Dropout(丢弃法,常用于神经网络)
Dropout 是深度学习中特有的正则化方法,它在每次训练时随机“丢弃”一部分神经元(即让它们的激活值变为0),从而降低对特定神经元的依赖,提高泛化能力。
- 实现:训练时,每个神经元以一定概率 置为 0,而在测试时保持完整网络。
- 效果:防止神经网络对某些特定路径的过度依赖,提高泛化能力。
- 应用:在 CNN、RNN、Transformer 等深度学习模型中广泛使用。
5. Batch Normalization(批量归一化)
虽然 Batch Normalization(BN)主要用于加速训练,但它也有正则化的效果:
- 通过对每个 mini-batch 进行归一化,使得数据分布更加稳定。
- 由于 BN 在训练时加入了一定的噪声(每个 mini-batch 计算的均值和方差略有不同),这起到了类似 Dropout 的正则化作用。
6. 数据增强(Data Augmentation)
数据增强是一种间接的正则化方法,它通过增加训练样本的多样性来减少过拟合。例如:
- 图像处理:随机旋转、翻转、裁剪、颜色变换等。
- 自然语言处理(NLP):同义词替换、词顺序打乱、数据扩增等。
- 语音处理:音频加噪声、时间拉伸等。
数据增强能让模型看到更多不同的变体,提高泛化能力。
7. 早停(Early Stopping)
在训练过程中,我们通常会监控验证集的损失,如果在某个点之后损失不再降低(甚至上升),说明模型开始过拟合训练集。这时我们可以提前停止训练,这就叫 Early Stopping。
- 优势:无需额外的正则化项,只需要监控损失即可。
- 劣势:需要一个合适的停止准则,否则可能会停止得太早或太晚。
正则化方法对比
| 正则化方法 | 主要作用 | 适用场景 |
|---|---|---|
| L1 正则化(Lasso) | 让部分权重变成 0(稀疏性),用于特征选择 | 线性模型、特征稀疏化 |
| L2 正则化(Ridge) | 让所有权重变小,提高稳定性 | 线性模型、深度学习(权重衰减) |
| Elastic Net | 结合 L1 和 L2 的优势 | 适用于高度相关特征 |
| Dropout | 随机丢弃神经元,减少过拟合 | 深度学习(CNN、RNN、Transformer) |
| Batch Normalization | 归一化输入,带来一定正则化效果 | 深度学习 |
| 数据增强 | 扩展数据集,提高泛化能力 | 计算机视觉、NLP、语音处理 |
| 早停(Early Stopping) | 监控验证集损失,避免过拟合 | 适用于所有训练过程 |
如何选择正则化方法?
- 线性模型(回归、SVM 等):
- 如果希望特征选择:L1 正则化(Lasso)
- 如果希望模型稳定性:L2 正则化(Ridge)
- 如果特征很多且高度相关:Elastic Net
- 深度学习(神经网络):
- Dropout:简单有效的正则化方式,尤其适用于全连接层。
- Batch Normalization:适用于大部分神经网络,提高训练稳定性,并提供一定的正则化作用。
- L2 正则化(Weight Decay):对所有参数进行约束,防止参数过大。
- 数据增强:计算机视觉、NLP、语音任务中不可或缺的正则化方法。
- Early Stopping:最简单的正则化方法,适用于所有模型。
Sinkhorn Distance 和 Wasserstein Distance
Wasserstein Distance 和 Sinkhorn Distance 都是衡量概率分布之间差异的度量,它们在计算机视觉、机器学习和计算几何等领域中都有广泛的应用。两者都来源于最优传输理论(Optimal Transport),但在计算效率和具体定义上有所不同。
1. Wasserstein Distance
Wasserstein距离,又叫做地球搬运者距离(Earth Mover’s Distance, EMD),衡量的是两个概率分布之间的最优“运输”成本。它的定义与运输问题类似:你可以将一个分布视为需要移动的“土堆”,另一个分布视为目标地,Wasserstein距离就是将一个分布移动到另一个分布的最小成本。
对于一维离散分布,Wasserstein-1距离定义为:
其中:
- 和 是两个概率分布,
- 是所有将分布映射到分布的联合分布集合(即所有可能的传输计划),
- 表示期望,是和之间的距离(通常取欧氏距离)。
简而言之,Wasserstein距离测量的是将一个分布通过最优传输“移动”到另一个分布所需要的成本。
2. Sinkhorn Distance
Sinkhorn距离是Wasserstein距离的一种正则化形式,它在计算中引入了一个熵正则化项,目的是加快计算速度并且使得计算变得更加稳定。
Sinkhorn距离通过在最优传输问题的目标函数中添加熵项来逼近Wasserstein距离。这使得计算上更加高效,尤其是在高维空间或大规模数据集上。
Sinkhorn距离的公式为:
其中:
是正则化参数,控制熵项的影响,时,Sinkhorn距离逼近Wasserstein距离,
是联合分布的熵,定义为:
通过增加熵正则化,Sinkhorn距离变得更加平滑,避免了计算Wasserstein距离时的直接复杂度,特别适用于大规模数据和计算资源有限的场景。
对比
| 特性 | Wasserstein Distance | Sinkhorn Distance |
|---|---|---|
| 定义 | 通过最优传输衡量概率分布间的最小传输成本。 | Wasserstein距离的正则化版本,添加了熵项以加速计算。 |
| 计算复杂度 | 计算复杂度较高,尤其是在高维空间。 | 通过引入熵正则化,计算更加高效。 |
| 正则化 | 无熵正则化。 | 有熵正则化参数,使得计算更加平滑。 |
| 应用场景 | 用于精确计算分布间的距离,适合低维、小规模数据。 | 适合大规模数据集和高维空间,能够有效降低计算复杂度。 |
总结
- Wasserstein Distance 是最优传输的经典度量,能够精确地衡量两个概率分布之间的差异,适用于需要高精度距离的场景。
- Sinkhorn Distance 通过引入熵正则化项,提供了一个高效且稳定的计算方法,特别适合大规模数据和复杂场景。
Tokenizer
“Tokenizer” 是一个处理文本的工具或过程,主要用于将文本数据拆分成更小的单元,这些单元可以是单词、子词、字符等,具体拆分方式取决于所使用的tokenizer类型。
在自然语言处理(NLP)和深度学习中,tokenizer 通常用于将原始文本转换为模型可以理解的格式。它的主要作用是将语言文本转化为“token”,即可供模型处理的基本单位。
常见的 Tokenizer 类型
基于空格分割的 Tokenizer: 这种方法通过空格来分割单词。它简单直接,适用于那些词汇边界很明显的语言(例如英语)。例如:
- 输入:“I love AI”
- 输出:
["I", "love", "AI"]
字符级 Tokenizer: 将文本拆分成单个字符。这种方法在某些语言(例如中文)或字符级任务中非常有用。
- 输入:“hello”
- 输出:
["h", "e", "l", "l", "o"]
子词级 Tokenizer(例如BPE): 将文本拆分成词或词的一部分。子词分割特别适合处理未知词(out-of-vocabulary words),减少词汇表的大小。BPE(Byte Pair Encoding)和WordPiece是两种常见的子词分割算法。
- 输入:“unhappiness”
- 输出:
["un", "happiness"](注意,子词级 tokenizer 会根据训练数据的词汇表来决定如何拆分。)
基于规则的 Tokenizer: 这类tokenizer依据预定义的规则进行文本拆分,规则可能包括标点符号、大小写等特征。这种方法对于某些复杂的文本任务更为精准。
预训练模型的 Tokenizer: 在现代NLP任务中,许多基于深度学习的预训练模型(如BERT、GPT、T5等)都有自己的tokenizer。这些tokenizer通常是基于WordPiece或BPE的,它们会根据词汇表将文本拆分成子词单元,方便模型处理。
为什么 Tokenizer 很重要?
- 处理未知词汇:通过子词分割,即使是模型没有见过的词汇,也能通过拆分成子词来处理。例如,“unhappiness” 可以被拆分为 “un”, “happiness”,这可以减少词汇表的大小,降低模型的复杂度。
- 标准化文本:Tokenizer 可以去除文本中的不必要的符号、空格、大小写等,帮助标准化输入,避免模型对格式化不一致的文本产生偏差。
- 输入向量化:文本通过tokenizer转化为tokens后,通常会进一步映射到数值表示(如词嵌入),以便供机器学习模型使用。
例子
在使用BERT模型时,BERT有一个专门的tokenizer,它会把输入的句子转换成词或子词token并给出对应的索引。例如:
- 输入:“I love AI”
- Tokenizer 输出:
["I", "love", "AI"]对应的索引可能是[101, 2003, 2293, 102]。
有些tokenizer还会标注特殊的起始符号 ([CLS]),分隔符 ([SEP]),或者填充符号 ([PAD]),这些都是为了帮助模型理解输入文本的结构。
Logits
在机器学习和深度学习中,logits 是指神经网络最后一层(未经过激活函数处理)的原始输出值,通常用于分类任务。在进行分类任务时,logits 通常会被送入 Softmax 或 Sigmoid 等激活函数,以转换为概率分布。
1. Logits 的数学定义
假设一个神经网络用于 类分类任务,其输出层有 个神经元。那么对于一个输入样本 ,神经网络的最后一层(全连接层)的输出为:
其中:
- 是权重矩阵,
- 是偏置向量,
- 就是 logits,它的大小是一个 维的向量。
logits 没有经过激活函数处理,因此可能包含任意实数值(正数、负数或零)。
2. Logits 与概率分布
在分类任务中,logits 通常需要通过 Softmax 函数转换成概率分布:
其中:
- 是第 个类别的 logits,
- 是第 个类别的预测概率。
例如:
- 如果 logits =
[2.0, 1.0, -1.0],那么经过 Softmax 变换后可能变为[0.65, 0.30, 0.05],表示模型预测第一个类别的概率最高。
对于二分类问题,logits 也可以通过 Sigmoid 函数转换为概率:
其中:
- 如果 很大, 接近 1,表示预测为正类。
- 如果 很小, 接近 0,表示预测为负类。
3. Logits 在知识蒸馏(Knowledge Distillation, KD)中的作用
在 知识蒸馏(KD) 过程中,学生模型(Student Model) 需要学习 教师模型(Teacher Model) 的知识,而 logits 是传递知识的重要方式。
原始的硬标签学习(Hard Labels Learning):
- 传统监督学习仅使用 ground truth 标签(如 one-hot 标签)来训练。
- 例如, 表示样本属于第 1 类。
知识蒸馏中的软标签(Soft Labels):
- 教师模型输出的 logits 经过 Softmax(带温度调节)后形成“软标签”:
- 这里的 是温度参数(Temperature),用于调整 logits 的分布。
- 较大的 会让分布更平滑,使得学生模型更容易学习不同类别之间的关系。
示例: 如果教师模型的 logits 是 [3.2, 1.5, -0.8]:
- 当 (标准Softmax):转换后可能是
[0.75, 0.22, 0.03]。 - 当 (温度调节Softmax):转换后可能是
[0.45, 0.35, 0.20],分布更平滑。
4. 为什么 Logits 很重要?
- 相比于 One-Hot 目标,Logits 包含更多信息:
- 传统分类训练只关注正确类别,而 logits 还能告诉模型“错误类别之间的关系”。
- 例如:
- One-hot 标签可能是
[1, 0, 0],但 logits 可能是[3.5, 2.8, -1.0],这表明第二类比第三类更接近第一类。
- One-hot 标签可能是
- 知识蒸馏(KD)利用 Logits 进行软目标学习:
- 学生模型可以通过蒸馏损失(Distillation Loss)来模仿教师模型的 logits,而不仅仅是正确类别的硬标签。
- 典型的蒸馏损失: 其中:
- 是教师模型的软目标概率。
- 是学生模型的预测概率。
- Logits 可用于对抗学习与解释性分析:
- 在对抗训练中,logits 的变化可以用于检测模型的鲁棒性。
- 在 NLP 任务中,logits 可以用于解释模型对某个输入的信心程度。
5. 直观理解
可以用一个 投票系统 来类比 logits:
- One-hot 标签:类似于“绝对胜利”,例如
{"猫": 1, "狗": 0, "兔子": 0},意味着 100% 确定是“猫”。 - Logits:类似于“投票评分”,例如
{"猫": 3.2, "狗": 1.5, "兔子": -0.8},表示“猫”得分最高,但“狗”也有一定的相关性。 - Softmax 后的概率:类似于“投票占比”,例如
{"猫": 75%, "狗": 22%, "兔子": 3%}。
通过 logits,模型不仅知道最终答案是什么,还能知道 其他类别的相对重要性,这对模型优化、知识蒸馏和可解释性研究都非常重要。
6. 总结
| 概念 | 描述 |
|---|---|
| Logits | 模型最后一层的原始输出(未经过激活函数) |
| Softmax | 用于将 logits 转换为概率分布 |
| Sigmoid | 二分类任务中用于归一化 logits |
| KD中的作用 | 用作“软标签”以帮助学生模型学习教师模型的知识 |
| 温度调节 | 通过调整 让 logits 分布更平滑,提高学生模型的学习效果 |
一句话总结
Logits 是神经网络输出的原始值,在知识蒸馏中用于提供比 one-hot 标签更丰富的信息,帮助学生模型更有效地学习教师模型的知识。
知识蒸馏(Knowledge Distillation, KD)常见问题与改进方向
知识蒸馏(Knowledge Distillation, KD)是一种模型压缩方法,它通过让 小模型(Student Model) 学习 **大模型(Teacher Model)**的知识,使得小模型在保持较高精度的同时降低计算复杂度。然而,KD 在实际应用中仍然存在一些挑战,并有许多改进方向来提升其性能。
1. 知识蒸馏常见问题
尽管 KD 方法在许多任务中取得了成功,但仍然面临以下挑战:
1.1. 软目标信息损失
问题:
- 传统 KD 方法使用 Soft Labels(软目标)作为监督信号,但小模型通常难以学习复杂的 logits 分布,导致信息损失。
- 对于极端不均衡的分类任务,Soft Labels 可能包含过多噪声或缺乏有效的类别区分度。
可能的改进:
- 多温度调节(Adaptive Temperature Scaling):调整蒸馏温度,使得不同类别的 logits 分布更加平滑,以便学生模型更容易学习知识。
- 类别感知蒸馏(Class-aware Distillation):对不同类别采用不同的温度,以避免某些类别信息过于模糊。
1.2. 训练不稳定
问题:
- 由于学生模型的容量较小,它可能难以完全模仿教师模型的行为,导致训练过程不稳定,甚至可能出现梯度爆炸或收敛缓慢。
可能的改进:
- 渐进式蒸馏(Progressive Distillation):从简单任务开始训练学生模型,然后逐步增加任务复杂度,使其更容易学习知识。
- 噪声鲁棒蒸馏(Robust KD with Noise Injection):在训练过程中引入噪声,增强模型的泛化能力,减少过拟合风险。
1.3. 任务不匹配(Mismatch between Teacher & Student)
问题:
- 由于学生模型和教师模型的结构可能存在较大差异(例如 CNN vs Transformer),学生模型可能难以直接学习教师模型的知识,导致蒸馏效率较低。
可能的改进:
- 跨架构蒸馏(Cross-Architecture Distillation):在不同架构之间引入 中间特征对齐(Intermediate Feature Matching) 或 相似度约束(Similarity Constraints)。
- 多教师蒸馏(Multi-Teacher Distillation):使用多个教师模型提供多种知识,从而提升学生模型的学习能力。
1.4. 仅依赖 Logits 信息,不充分利用教师模型的知识
问题:
- 经典 KD 方法(如 Hinton 提出的 KD)主要关注 logits 输出,而忽略了教师模型的中间特征表示,导致学生模型未能充分学习教师模型的深层知识。
可能的改进:
- 特征蒸馏(Feature-based Distillation):不仅学习教师的最终 logits 输出,还让学生模型学习教师模型的中间层特征,使得学生能够更好地理解任务特征。
- 关系蒸馏(Relation-based Distillation):让学生学习教师模型中不同样本之间的关系,而不仅仅是 logits 分布。
1.5. 计算资源消耗大
问题:
- 知识蒸馏通常需要同时训练教师和学生模型,这对计算资源要求较高,尤其是当教师模型较大(如 GPT-4, ViT-32B)时,计算成本显著增加。
可能的改进:
- 离线蒸馏(Offline Distillation):预先计算教师模型的输出,存储下来并供学生模型使用,避免训练时重复计算教师模型的预测结果。
- 在线蒸馏(Online Distillation):在训练过程中同时训练多个学生模型,使其互相学习,从而降低对大教师模型的依赖。
2. 知识蒸馏的改进方向
针对上述问题,研究者们提出了多种改进方法来提升知识蒸馏的效果:
2.1. 多任务蒸馏(Multi-Task Distillation)
- 结合多个任务的知识进行蒸馏,使得学生模型能够同时学习多个不同的任务,提升其泛化能力。
- 示例:
- 在 NLP 任务中,让学生模型同时学习分类、序列生成和命名实体识别(NER)。
2.2. 关系蒸馏(Relational Knowledge Distillation)
- 让学生不仅学习教师的单个样本输出,还要学习教师对不同样本的关系,例如样本之间的相似性。
- 示例:
- 在图像分类任务中,可以让学生学习教师模型对不同类别的样本之间的余弦相似度。
2.3. 自蒸馏(Self-Distillation)
- 让同一个模型(或者不同层之间)进行蒸馏,使得浅层学习深层的信息,从而提升模型的表现。
- 示例:
- 在 CNN 网络中,让浅层特征向深层特征学习,使得整个网络的特征表达更加鲁棒。
2.4. 对抗蒸馏(Adversarial Knowledge Distillation, AKD)
- 采用对抗训练方法,在蒸馏过程中引入对抗样本,使得学生模型对分布变化更加鲁棒。
- 示例:
- 在图像识别中,使用对抗攻击生成的样本进行蒸馏,使得学生模型具有更好的对抗攻击防御能力。
2.5. 知识融合蒸馏(Ensemble Distillation)
- 结合多个教师模型(如 CNN+Transformer 或多个不同预训练模型)进行蒸馏,使得学生模型可以学习多个模型的优势。
- 示例:
- 在语音识别任务中,结合 Transformer 和 RNN 作为教师模型,从而提升学生模型的效果。
2.6. 生成式知识蒸馏(Generative Knowledge Distillation)
- 让学生模型不仅仅依赖于训练数据,还能够生成新的数据进行自监督学习,从而减少对标注数据的依赖。
- 示例:
- 在 NLP 任务中,使用教师模型生成伪数据,并让学生模型同时学习真实数据和伪数据。
3. 总结
| 问题 | 改进方向 |
|---|---|
| 软目标信息损失 | 采用自适应温度调整(Adaptive Temperature)、类别感知蒸馏(Class-aware Distillation) |
| 训练不稳定 | 渐进式蒸馏(Progressive Distillation)、噪声鲁棒蒸馏(Robust KD) |
| 任务不匹配 | 跨架构蒸馏(Cross-Architecture KD)、多教师蒸馏(Multi-Teacher KD) |
| 仅依赖 logits | 特征蒸馏(Feature KD)、关系蒸馏(Relation KD) |
| 计算资源消耗大 | 离线蒸馏(Offline KD)、在线蒸馏(Online KD) |
| 知识利用不足 | 多任务蒸馏(Multi-task KD)、自蒸馏(Self KD)、对抗蒸馏(Adversarial KD) |
神经网络中的常见层及其数学原理
神经网络中有多种类型的层,每种层有其特定的数学原理、适用条件和作用。以下是常见的几种层类型的详细解释:
1. 全连接层(Fully Connected Layer, FC)
数学原理
全连接层是最基础的神经网络层类型,每个输入神经元与输出神经元相连接,常用于处理线性和非线性问题。
假设输入向量为 ,权重矩阵为 ,偏置为 ,全连接层的输出 可以表示为:
然后,通常应用一个激活函数 来引入非线性:
适用条件
- 适用于需要将输入的所有特征进行加权和组合的情况。
- 通常用在神经网络的最后几层,进行全局信息汇总。
作用
- 用于将高维的输入数据压缩成一个低维的表示,或者将低维数据映射到更高维的空间。
- 适合于结构简单的任务(如图像分类、回归任务等)。
2. 卷积层(Convolutional Layer, Conv)
数学原理
卷积层用于从输入中提取局部特征(如图像中的边缘、纹理等)。其核心操作是卷积运算。假设输入图像为 ,卷积核为 ,卷积的输出 可以表示为:
其中 表示卷积操作。卷积是滑动窗口操作,每次使用卷积核对局部区域进行加权求和,并输出一个特征值。
适用条件
- 主要用于图像处理、视频分析、语音识别等任务。
- 适合具有空间结构的输入数据(如图像、时间序列等)。
作用
- 提取局部特征:卷积操作可以捕捉图像中的局部空间关系(如边缘、角点、纹理等)。
- 权重共享:同一个卷积核在整个输入上滑动,减少了参数量,增强了模型的泛化能力。
- 多层卷积可以捕捉从低级到高级的复杂特征。
3. 池化层(Pooling Layer)
数学原理
池化层用于对输入的特征图进行下采样,减少数据的维度,减小计算量,并保留最重要的特征。常见的池化方法有:
- 最大池化(Max Pooling):取局部区域的最大值:
- 平均池化(Average Pooling):取局部区域的平均值:
其中, 是池化窗口的大小。
适用条件
- 适用于图像、时间序列等需要进行降维的任务。
- 一般放在卷积层之后,用于减小特征图的尺寸。
作用
- 降维:减少计算复杂度,减小网络的内存需求。
- 特征提取:池化层帮助模型选择最显著的特征,增强模型的鲁棒性(对平移、缩放等变换的鲁棒性)。
- 减少过拟合:通过池化降低数据的精度,使模型更为稳健。
4. 归一化层(Normalization Layer)
数学原理
归一化层通常用于规范化输入数据,帮助加速训练并提高模型的稳定性。常见的归一化方法包括:
- 批量归一化(Batch Normalization, BN):对每一层的输入进行标准化,使得输入的均值为 0,方差为 1。假设某层的输入为 ,批量归一化操作为: 其中, 和 分别是批量数据的均值和标准差。
- 层归一化(Layer Normalization, LN):与 BN 类似,但 LN 是在每个样本的每一层进行归一化,而不是在一个 mini-batch 上进行。
适用条件
- 批量归一化(BN) 适用于有多个样本的任务(如图像分类)。
- 层归一化(LN) 适用于 RNN 和 Transformer 等序列模型,特别是处理小批量数据时。
作用
- 加速训练:减少权重初始化的影响,加快收敛速度。
- 减少梯度消失和梯度爆炸问题:通过标准化输入,有助于缓解梯度问题。
- 提高稳定性:增强网络在不同训练阶段的稳定性,避免激活值过大或过小。
5. 注意力层(Attention Layer)
数学原理
注意力机制通过计算输入序列的加权和来决定哪些部分对当前任务最重要,常见的计算方法有:
- 自注意力(Self-Attention):对输入序列的每个位置进行加权,使得模型能够关注到其他位置的信息。对于给定的输入 ,自注意力计算为: 其中, 是查询(Query), 是键(Key), 是值(Value), 是键的维度。
适用条件
- 用于处理序列数据(如文本、语音)中的长期依赖问题。
- 特别适用于 Transformer 模型和其他基于自注意力的架构。
作用
- 捕捉长程依赖:通过计算全局的注意力权重,模型能够在一个序列中不同位置之间建立关联。
- 灵活性:模型可以动态地关注不同部分的信息,从而增强表达能力。
- 并行计算:与传统的 RNN 和 LSTM 不同,注意力机制允许并行计算,提高了训练效率。
6. 递归层(Recurrent Layer)
数学原理
递归层(如 LSTM、GRU)用于处理序列数据,能够保持一定的“记忆”信息。以 LSTM 为例,它的基本操作通过一个单元的多个门(门控机制)来控制信息的流动:
适用条件
- 适用于处理时间序列、文本等具有时序特征的数据。
- 在处理具有长期依赖的问题时,LSTM 和 GRU 更为有效。
作用
- 捕捉时间序列数据的依赖关系:适用于需要记住历史信息的任务(如语音识别、机器翻译等)。
- 缓解梯度消失问题:通过门控机制,LSTM 和 GRU 能够更好地捕捉长时间序列中的依赖关系。
自回归(Auto-Regressive)属性
- 自回归(Auto-Regressive)模型 是指每个时间步的输出仅依赖于之前时间步的输入和输出,而不会提前获取未来信息。
- 例如,在语言生成任务中(如机器翻译、文本生成),模型在生成第 i 个单词时,只能看到前 i-1 个单词,不能直接访问未来的单词,否则会导致数据泄漏(data leakage)。
在 Transformer 解码器中,如果不加限制,自注意力(Self-Attention) 机制可能会让每个位置的信息自由流动,导致未来单词的信息影响当前单词的预测,破坏自回归特性。
ReLU
ReLU(Rectified Linear Unit,修正线性单元)激活函数的数学表达式如下:
Tokenizer 在 Transformer 模型中的位置
Tokenizer(分词器) 是 Transformer 模型输入预处理的一部分,它位于 模型架构之外,用于将原始文本转换为模型可处理的 Token(标记)序列。在实际流程中,Tokenizer 在 Transformer 的 Input Embedding 之前,其作用是将原始的输入文本转换为模型可以理解的数值表示。
1. Tokenizer 在 Transformer 处理流程中的位置
Transformer 主要由以下步骤组成:
- 输入文本(原始字符串)
- Tokenizer(分词器):将文本转换为 Token ID 序列
- Input Embedding(词嵌入层):将 Token ID 转换为向量
- Positional Encoding(位置编码)
- Transformer Encoder / Decoder(核心计算)
- Prediction Head(Softmax 计算输出)
- 输出 Token ID,再经过 Tokenizer 反向映射,转换回文本
在 Transformer 模型架构图中,Tokenizer 并不在模型本身内部,而是模型的 前处理 和 后处理 部分。
2. Tokenizer 作用
- 分词(Tokenization):将输入文本拆分成 Token(如
"I love NLP"→["I", "love", "NLP"])。 - 子词编码(Subword Encoding):例如使用 BPE、WordPiece、SentencePiece 进行子词拆分(如
"playing"→["play", "##ing"])。 - 映射为 Token ID(Mapping to Token IDs):将 Token 转换为数值,如:
["I", "love", "NLP"] → [101, 1045, 2293, 7896, 102] - 填充(Padding) 和 截断(Truncation):调整输入长度,使其匹配 Transformer 的输入大小。
- 添加特殊 Token(如 [CLS], [SEP]):用于分类任务或分隔不同句子。
- Tokenizer 放在哪里?
从软件实现的角度,Tokenizer 通常放在 Transformer 模型的输入处理环节,常见于:
- 在 文本输入到 Transformer 之前执行
- 在 数据加载(Dataloader)或预处理(Preprocessing)部分
- 在 推理(Inference)时,模型输出 Token ID 后再用 Tokenizer 还原文本
示例代码
from transformers import AutoTokenizer, AutoModel
# 加载 Tokenizer
tokenizer = AutoTokenizer.from_pretrained("bert-base-uncased")
# 输入文本
text = "Hello, how are you?"
# Tokenization
tokens = tokenizer(text, return_tensors="pt")
# 送入 Transformer 模型
model = AutoModel.from_pretrained("bert-base-uncased")
output = model(**tokens)
在该示例中:
- tokenizer(text) 负责前处理
- model(**tokens) 负责 核心计算
- tokenizer.decode(output_ids) 负责后处理
- Tokenizer 在不同 Transformer 任务中的作用
(1) 语言模型(GPT、BERT)
- 输入: 句子 → Tokenizer → Token ID → Transformer
- 输出: Token ID → Tokenizer 解码 → 句子
(2) 机器翻译(T5、BART)
- 输入: 英文 → Tokenizer → Token ID → Transformer
- 输出: 法文 Token ID → Tokenizer 解码 → 法文文本
(3) 文本分类(BERT for Classification)
- 输入: [CLS] + 句子 + [SEP] → Tokenizer
- 输出: Transformer 处理 [CLS] token,输出分类标签
- 结论
- Tokenizer 是 Transformer 输入的前处理步骤,不属于模型本体,而是用于文本到数值的转换。
- Tokenizer 的输出是 Token ID,传入 Input Embedding 后进入 Transformer 计算。
- 模型输出 Token ID 后,还需要 Tokenizer 反向解码回文本。
- 在 PyTorch、TensorFlow、Hugging Face Transformers 框架中,Tokenizer 是 Transformer 交互的关键组件。
交叉熵损失如何监督 Transformer 训练
在 Transformer 训练过程中,交叉熵损失(Cross-Entropy Loss)用于衡量模型的预测输出与真实标签之间的误差,并通过梯度反向传播来更新模型参数。它是 Transformer 任务(如机器翻译、文本生成、语言建模)中最常用的损失函数。
1. 交叉熵损失的作用
- 衡量预测与真实标签的差距:计算 Transformer 预测 Token 分布与真实 Token 之间的误差。
- 指导梯度更新:通过反向传播(Backpropagation)计算梯度,使 Transformer 逐步优化权重。
- 提升模型在训练集上的拟合能力:交叉熵损失减少错误预测,提高模型的生成质量。
2. 交叉熵损失的计算步骤
(1) 前向传播(Forward Propagation)
- 输入:真实文本 Token(经过 Tokenizer 处理)。
- 嵌入(Embedding):输入 Token 经过嵌入层转换为向量。
- Transformer 计算:经过多个注意力层、前馈层,得到最终隐藏状态。
- 线性层(Linear Projection):将隐藏状态映射到词汇表维度,生成 logits: 其中:
- 是 Transformer 解码器在时间步 的输出 logits。
- 是输出层的权重矩阵(隐藏层维度 → 词汇表大小)。
- 是 Transformer 计算的隐藏状态。
(2) Softmax 归一化
- 将 logits 转换为概率分布: 其中:
- 是词汇表中第 个单词的概率。
- 目标是让 Transformer 预测的概率 更接近真实 Token 的分布 。
(3) 计算交叉熵损失
- 交叉熵衡量真实 Token 分布 和 Transformer 预测分布 之间的差距:
- 在 NLP 任务中,真实分布 采用 one-hot 编码:
- 交叉熵损失可以简化为: 即只计算真实 Token 位置上的概率值。
3. 交叉熵如何用于监督 Transformer 训练
(1) 计算损失
在 PyTorch 中,交叉熵损失可以使用 torch.nn.CrossEntropyLoss() 计算:
import torch
from torch.nn import CrossEntropyLoss
loss_fct = CrossEntropyLoss()
loss = loss_fct(logits.view(-1, vocab_size), labels.view(-1))
- ogits.view(-1, vocab_size):将 Transformer 预测的 logits 调整为形状 (batch_size * seq_len, vocab_size)。
- labels.view(-1):将真实标签转换为 (batch_size * seq_len,),以便计算交叉熵。
(2) 计算梯度(反向传播)
- 计算损失后,使用 反向传播 计算梯度:
loss.backward() # 计算梯度
optimizer.step() # 更新参数
- 损失越大,梯度越大,参数更新幅度越大。
- 损失越小,说明 Transformer 的预测更接近真实标签。
4. Transformer 训练过程中交叉熵损失的优化作用
(1) 通过梯度下降优化参数
- 交叉熵损失计算误差,并通过 反向传播(Backpropagation) 计算梯度:
其中:
- 是 Transformer 的参数(如注意力权重)。
- 是学习率。
- 是交叉熵损失对参数的梯度。
(2) 逐步收敛
- 初始阶段:交叉熵损失较高,模型预测的 Token 可能是随机的。
- 训练中期:Transformer 开始学习 Token 之间的关系,损失下降。
- 训练后期:交叉熵损失收敛,Transformer 预测结果更准确。
(3) 交叉熵损失的变化趋势
- 理想情况下:交叉熵损失随训练轮数逐步下降。
- 过拟合风险:如果训练损失下降但验证损失上升,可能是 Transformer 过拟合训练数据。
5. Transformer 任务中的交叉熵损失示例
(1) 语言建模(GPT、BERT)
- 目标:预测 Masked Token 或下一个 Token。
- 交叉熵计算方式:
- 监督训练过程:
- 模型预测 logits。
- 计算 Softmax 概率。
- 计算预测 Token 与真实 Token 之间的交叉熵损失。
- 反向传播更新 Transformer 参数。
(2) 机器翻译(T5、BART)
- 目标:翻译句子。
- 交叉熵计算方式:
- 监督训练过程:
- 输入源语言 。
- 目标语言 作为 labels。
- 计算 Transformer 输出的 logits。
- 计算交叉熵损失。
- 反向传播更新 Transformer 权重。
Optimal Transport (OT) Matrix(最优传输矩阵)
1. 什么是 Optimal Transport(最优传输)?
最优传输(Optimal Transport, OT) 是一个数学框架,旨在测量两个概率分布之间的距离,并寻找从一个分布转移到另一个分布的最优方式。它在 深度学习、计算机视觉、自然语言处理和概率推理 等领域有广泛应用。
Optimal Transport Matrix(最优传输矩阵) 是 OT 问题中的核心概念,它表示如何在最小成本的情况下,将一个源分布的质量分配到目标分布上。
2. 最优传输问题的数学表述
2.1 问题定义
给定两个离散概率分布:
- 源分布 ,定义在 个点上,满足 。
- 目标分布 ,定义在 个点上,满足 。
以及一个 代价矩阵(Cost Matrix) ,其中 代表将质量从点 传输到点 的代价。
2.2 目标函数
寻找一个 传输矩阵(Transport Matrix) ,使得总运输成本最小:
约束条件:
- 保持总量守恒(即必须将所有质量都传输完):
- 非负性: 不能有负的运输量。
3. 最优传输矩阵的计算方法
在实际应用中,求解 最优传输矩阵 主要有以下几种方法:
🔹 3.1 线性规划(Linear Programming, LP)
- 经典的 Wasserstein 距离(Earth Mover’s Distance, EMD)求解方法。
- 使用线性规划求解: 约束:
- 缺点:计算复杂度较高,通常为 。
🔹 3.2 Sinkhorn-Knopp 迭代(Sinkhorn Distance)
- 引入熵正则化(Entropy Regularization),优化计算效率: 其中 控制正则化强度,增加熵项能使矩阵 更加平滑。
- 优点:大幅降低计算复杂度,可并行化计算,适用于深度学习任务。
🔹 3.3 近似算法
- Wasserstein GAN:利用最优传输度量改进生成对抗网络(GAN)的稳定性。
- Gromov-Wasserstein Distance:用于比较不同空间中的分布。
4. Optimal Transport Matrix 的应用
(1)深度学习与生成模型
- Wasserstein GAN(WGAN):用 Wasserstein 距离 代替 JS 散度,提高生成质量。
- 域适配(Domain Adaptation):计算两个数据分布的 OT 矩阵,实现无监督迁移学习。
(2)自然语言处理(NLP)
- 词向量对齐(Word Embedding Alignment):用 OT 计算不同语言的词嵌入之间的映射。
- 句子匹配(Sentence Similarity):使用 Wasserstein 距离计算两个句子的语义相似性。
(3)计算机视觉
- 图像匹配:通过 OT 计算两个图像的特征分布差异。
- 风格迁移:用 OT 计算源图像与目标图像的特征映射关系。
5. 结论
✅ Optimal Transport Matrix 是用于解决分布匹配问题的数学工具,核心思想是在最小传输成本下,将源分布映射到目标分布。
✅ 计算 Optimal Transport 的方法包括 线性规划、Sinkhorn-Knopp 迭代、近似方法。
✅ 在 深度学习、计算机视觉、NLP 等领域,OT 被广泛用于度量分布相似性、域适配、GAN 训练等任务。
dim_feedforward
dim_feedforward 是 Transformer 架构中的一个重要超参数,代表 前馈全连接网络(Feed Forward Network,FFN) 隐藏层的维度。它通常设置为 d_model 的几倍(例如:4 倍),用来控制前馈网络的容量和处理能力。
前馈全连接网络(Feed Forward Network)
在 Transformer 中,每个 编码器 和 解码器 层都包含一个前馈网络。该网络通常由两层全连接层组成,并通过一个激活函数(通常是 ReLU)连接。
FFN 结构
一个前馈网络包含两个主要的部分:
- 第一层:输入维度为
d_model,输出维度为dim_feedforward。 - 第二层:将
dim_feedforward维度的输出映射回d_model,用于保持 Transformer 模型的维度一致性。
具体流程
- 输入:前馈网络的输入是经过 多头自注意力(Multi-Head Attention) 计算后得到的输出向量,其维度为
d_model。 - 第一层全连接:输入通过一个全连接层,输出维度变为
dim_feedforward,这是一个通常比d_model大的维度。这样做是为了让模型具有更大的表示能力。 - 激活函数:一般采用 ReLU 激活函数,使得网络更具非线性表达能力。
- 第二层全连接:将激活函数后的输出通过另一个全连接层映射回
d_model的维度,以确保最终输出与输入维度一致。 - 输出:最后的输出将传递到 LayerNorm(层归一化),然后继续传递到下一个编码器层或解码器层。
作用
dim_feedforward控制了前馈网络的 容量,即网络可以处理和表示信息的复杂度。更大的dim_feedforward会提高模型的表达能力,但也会增加计算复杂度和参数数量。dim_feedforward常设置为d_model的 4 倍。例如,若d_model = 128,则dim_feedforward通常设为 512。
例子
假设:
d_model = 128dim_feedforward = 512
那么,前馈网络的结构将会是:
- 输入维度是
128,输出维度是512。 - 然后通过 ReLU 激活函数,再将输出映射回
128维度。
总结
dim_feedforward是 Transformer 模型中的一个超参数,控制了前馈网络的隐藏层的维度。- 它对模型的 表示能力 和 计算复杂度 有直接影响。通过增加该值,模型可以学习到更复杂的特征,但同时也会增加计算量。
Transformer 的前馈神经网络(Feed Forward Network, FFN)
在 Transformer 的 前馈神经网络(Feed Forward Network, FFN) 中,包含 两个全连接层(FC 层),它们通过一个 激活函数(通常是 ReLU) 连接。结构如下:
FFN 结构
前馈神经网络(FFN)在 Transformer 的 每个编码器和解码器层 中都会出现,它的作用是对每个 token 的表示进行进一步的非线性变换,增强模型的表达能力。
数学公式
其中:
第一层全连接(FC1):
- 作用:将
d_model维度的输入扩展到dim_feedforward维度(通常是4 × d_model)。 - 激活函数:使用 ReLU(ReLU(x) = max(0, x))进行非线性变换。
- 作用:将
第二层全连接(FC2):
- 作用:将
dim_feedforward维度的隐藏层投影回d_model维度,以保持 Transformer 计算图中的一致性。
- 作用:将
数据流示例
假设:
d_model = 128dim_feedforward = 512
那么 FFN 的数据流如下:
- 输入:一个
128维向量 x - 第一层 FC(扩展):
- 维度变化:
128 → 512 - 计算:
W_1形状:128 × 512b_1形状:512
- 维度变化:
- 第二层 FC(投影回原维度):
- 维度变化:
512 → 128 - 计算:
W_2形状:512 × 128b_2形状:128
- 维度变化:
- 输出:
128维向量 y,传递到下一层 Transformer 计算。
PyTorch 代码实现
import torch
import torch.nn as nn
class FFN(nn.Module):
def __init__(self, d_model=128, dim_feedforward=512):
super(FFN, self).__init__()
self.fc1 = nn.Linear(d_model, dim_feedforward) # 第一层 FC
self.relu = nn.ReLU() # 激活函数
self.fc2 = nn.Linear(dim_feedforward, d_model) # 第二层 FC
def forward(self, x):
x = self.fc1(x) # 线性变换 (128 -> 512)
x = self.relu(x) # 非线性变换
x = self.fc2(x) # 线性变换 (512 -> 128)
return x
# 测试 FFN
ffn = FFN()
input_tensor = torch.randn(1, 128) # 假设 batch_size=1, 输入维度 128
output_tensor = ffn(input_tensor)
print(output_tensor.shape) # 预期输出: torch.Size([1, 128])
总结
- 第一层 FC(扩展) :d_model → dim_feedforward
- ReLU 激活 :引入非线性,使模型能学习复杂关系
- 第二层 FC(投影回原维度) :dim_feedforward → d_model
- 最终输出:与输入形状一致,便于传递给下一层 Transformer 计算 这样,FFN 在 Transformer 中通过 非线性扩展 + 线性投影 的方式,提高了模型的表达能力,同时保持了计算的稳定性和一致性。
低比特量化(Post-Training Quantization)
术语解释
定义:
低比特量化是一种模型压缩技术,旨在将训练好的深度学习模型中的权重和激活值从高精度(如32位浮点数)转换为低精度(如4位或8位整数),从而减少模型存储大小和计算开销,同时尽量保持模型性能。
核心原理:
- 训练后量化(PTQ):在模型训练完成后进行量化,无需重新训练或微调。
- 步骤:
- 校准:使用少量无标签数据统计权重/激活的分布(如最大值、最小值),确定量化范围。
- 映射:将浮点数值线性或非线性映射到低比特整数(如将[-1, 1]映射到4位整数0~15)。
- 反量化:推理时再将低比特整数恢复为浮点数进行运算。
- 难点:极低比特(如4-bit)会导致信息丢失严重,尤其是权重分布不均匀或激活存在异常值时。
- 步骤:
改进方法(如DuQuant):
- 权重变换:通过矩阵旋转或置换,使权重分布更均匀,减少量化误差。
- 动态截断:可学习截断阈值,保留重要权重,丢弃冗余值。
应用场景:
- 大模型部署:如将LLaMA-70B量化到4-bit,使其能在手机或边缘设备运行。
- 推理加速:低比特运算在GPU/TPU上可提升计算吞吐量。
优势与挑战:
- 优势:大幅减少模型内存占用和能耗。
- 挑战:低于8-bit时性能可能显著下降,需通过算法优化(如DuQuant)缓解。
LoRA(Low-Rank Adaptation,低秩适应)
定义:
LoRA是一种高效微调大模型的技术,通过向原始模型权重注入低秩矩阵(低维参数矩阵),仅训练这些新增的小参数来适配下游任务,避免全参数微调的计算成本。
核心原理:
- 低秩分解:假设模型权重更新(ΔW)可用低秩矩阵近似,即 ΔW = A×B,其中A∈ℝ^{d×r},B∈ℝ^{r×k},秩r≪d,k。
- 参数效率:仅需训练A和B(总参数量为r×(d+k)),远小于原权重矩阵的d×k。
- 微调过程:冻结原始权重W,仅更新A和B,公式为:输出 = Wx + (AB)x。
应用场景:
- 大模型适配:如GPT-3、扩散模型的跨领域微调(如Terra论文中的时变LoRA)。
- 多任务学习:为不同任务训练独立的LoRA模块,动态切换适配器。
优势与挑战:
- 优势:
- 计算高效:训练参数量减少90%以上,适合资源有限场景。
- 兼容性:可与其他技术(如量化)结合,进一步提升效率。
- 挑战:
- 秩的选择:秩r过小可能限制表达能力,需根据任务调整。
- 领域差异大时效果下降:需结合动态机制(如Terra的时间变量)增强灵活性。
实例关联:
- Terra:在扩散模型中引入时变LoRA,动态调整低秩矩阵以适应连续域变化。
- DuQuant:通过量化技术压缩LLM,而LoRA可进一步减少微调时的计算负担。
这两个技术分别从模型压缩和参数高效微调角度,推动大模型在实际场景中的应用。
量化(Quantization)
定义:
量化是将高精度(如32位浮点数)的模型参数或中间计算结果(激活值)转换为低精度表示(如8位整数)的过程。
量化作用:
- 减少内存占用:
- 例如:32位浮点 → 8位整数,内存占用减少至1/4。
- 加速计算:
- 整数运算速度远高于浮点运算,尤其在专用硬件(如NPU、TPU)中。
- 降低功耗:
- 低精度计算减少能耗,适合移动端或边缘设备部署。
- 兼容性提升:
- 部分硬件仅支持整数运算(如某些边缘芯片)。
代价:
- 精度损失:低精度表示可能引入误差,需通过算法优化(如DuQuant)缓解。
量化过程
步骤分解:
确定动态范围:
- 统计权重或激活值的最小值(min)和最大值(max)。
- 例如:某层激活值范围 [-5.3, 127.8]。
选择量化精度:
- 如8位整数(INT8)的范围为 [-128, 127] 或 [0, 255]。
计算量化参数:
- Scale(缩放因子):
scale = (max - min) / (quant_max - quant_min) - Zero Point(零点偏移):调整量化后的零点对齐原数据零点。
- 例如:将[-5.3, 127.8]映射到[0, 255],计算scale和zero point。
- Scale(缩放因子):
量化操作:
- 将浮点值映射到整数:
quantized_value = round((float_value - min) / scale) + zero_point
- 将浮点值映射到整数:
反量化(Dequantization):
- 将整数还原为浮点近似值:
dequantized_value = scale * (quantized_value - zero_point)
- 将整数还原为浮点近似值:
数学公式:
异常值(Outliers)
定义:
异常值是指数据集中显著偏离其他样本的极端值。在神经网络中,特指权重或激活值中数值远大于/小于其他值的元素。
在量化中的影响:
- 权重或激活值的异常值会增大动态范围(最大值与最小值的差),导致量化后的分辨率下降(步长变大)。
- 例如:某层激活值大部分在 [0, 1],但存在个别值高达 1000,直接量化会导致低精度区域(0-1)的表示过于粗糙。
示例:
- Normal Outliers:所有输入样本的某些通道持续存在高幅值(如LLM中FFN层的部分通道)。
- Massive Outliers:仅少数输入样本触发,但数值极大(如某些激活值达到中位值的千倍)。
激活值(Activation)
定义:
激活值是神经网络中某一层的输出结果,通常由输入数据经过线性变换(如矩阵乘法)和非线性激活函数(如ReLU、GELU)生成。
在量化中的关键性:
- 激活值的动态范围直接影响量化效果。例如:
- 若激活值范围波动大(存在异常值),量化误差会显著增加。
- 若激活值分布集中(如经过归一化),量化后精度损失较小。
示例:
- 在Transformer的FFN层中,激活值可能因异常输入触发极端值(Massive Outliers)。
异常值与量化的关系
问题根源:
- 若激活值中存在异常值(如某通道最大值远高于其他通道),量化后的分辨率会集中在异常值附近,导致常规区域(如中低幅值)的表示精度大幅下降。
解决方案(以DuQuant为例):
- 旋转变换:
- 通过矩阵旋转将异常值分散到多个通道,降低单通道的最大值。
- 置换重排:
- 按之字形(Zigzag)重排通道,平衡不同块间的异常值分布。
- 权重调整:
- 对权重矩阵应用逆变换,保持数学等价性,避免额外计算开销。
总结
- 异常值:极端偏离正常范围的数值,破坏量化分辨率。
- 量化:将高精度数据压缩为低精度表示,以节省资源。
- 激活值:网络层的输出结果,其分布直接影响量化效果。
- 量化过程:动态范围统计→参数计算→映射→反量化。
DuQuant
DuQuant通过**双变换(旋转变换 + 置换)**重新分布激活值中的异常值,降低量化难度。以下是其数学原理的逐步分解:
1. 问题建模
假设某层的激活值为 ( \mathbf{A} \in \mathbb{R}^{n \times d} )(n个token,d个通道),其中某些通道存在异常值。量化误差主要取决于激活值的动态范围(最大值与最小值的差)。目标是通过线性变换 ( \mathbf{T} ) 将 ( \mathbf{A} ) 转换为 ( \mathbf{A}’ = \mathbf{A} \mathbf{T} ),使得 ( \mathbf{A}’ ) 的动态范围更小,从而降低量化误差。
2. 旋转变换(Rotation Transformation)
目标:
将异常值分散到多个通道,降低单通道的最大值。
数学表示:
分块对角旋转矩阵:
将通道分为 ( k ) 个块(block),每个块大小为 ( b \times b ),构建分块对角矩阵:
[ \mathbf{R} = \begin{bmatrix} \mathbf{R}_1 & 0 & \cdots & 0 \ 0 & \mathbf{R}_2 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & \mathbf{R}_k \end{bmatrix}, \quad \mathbf{R}_i \in \mathbb{R}^{b \times b} \text{ 为旋转矩阵(正交矩阵)} ] 分块结构减少了计算复杂度,同时保持局部通道的相关性。优化目标:
对每个块 ( \mathbf{R}i ),通过贪心算法优化旋转方向,最小化块内最大激活值:
[ \min{\mathbf{R}i} \max{j} | (\mathbf{A}_i \mathbf{R}i){j} | ] 其中 ( \mathbf{A}_i ) 是原始激活矩阵的第 ( i ) 个块。
贪心算法步骤:
- 初始化 ( \mathbf{R}_i ) 为单位矩阵。
- 计算当前块的最大激活值 ( m )。
- 选择一对通道 ( (p, q) ),构造 Givens 旋转矩阵 ( \mathbf{G}(p, q, \theta) )(通过旋转角度 ( \theta ) 将部分能量从高激活通道 ( p ) 转移到低激活通道 ( q ))。
- 更新 ( \mathbf{R}_i \leftarrow \mathbf{R}_i \mathbf{G}(p, q, \theta) ),并重新计算 ( m )。
- 迭代直至 ( m ) 不再显著下降。
3. Zigzag置换(Permutation)
目标:
平衡不同块间的异常值分布,减少块间方差。
数学表示:
排列矩阵:
将通道按激活值大小以“之字形”模式重新排列,构造置换矩阵 ( \mathbf{P} )。例如,对于 ( d=8 ),排列顺序为 [1, 5, 2, 6, 3, 7, 4, 8],确保高激活通道分散到不同块中。置换后的激活矩阵:
[ \mathbf{A}” = \mathbf{A}’ \mathbf{P} = \mathbf{A} \mathbf{R} \mathbf{P} ]
效果分析:
置换操作使得每个块内的激活值分布更均匀,避免单个块因聚集过多异常值而增大动态范围。
4. 权重调整(Weight Adaptation)
为保持模型输出的数学等价性,需对权重矩阵 ( \mathbf{W} ) 进行逆变换。
数学推导:
原始层的计算为:
[ \mathbf{Y} = \mathbf{A} \mathbf{W} ] 应用变换后的计算为:
[ \mathbf{Y}’ = \mathbf{A}” \mathbf{W}’ = \mathbf{A} \mathbf{R} \mathbf{P} \mathbf{W}’ ] 为使 ( \mathbf{Y}’ = \mathbf{Y} ),需满足:
[ \mathbf{R} \mathbf{P} \mathbf{W}’ = \mathbf{W} \quad \Rightarrow \quad \mathbf{W}’ = (\mathbf{R} \mathbf{P})^{-1} \mathbf{W} = \mathbf{P}^\top \mathbf{R}^\top \mathbf{W} ] (注:由于 ( \mathbf{R} ) 是正交矩阵,( \mathbf{R}^{-1} = \mathbf{R}^\top ),且 ( \mathbf{P} ) 是置换矩阵,( \mathbf{P}^{-1} = \mathbf{P}^\top ))
5. 理论证明:降低激活方差
动态范围分析:
量化误差与激活值的动态范围(最大值与最小值之差)成正比。通过旋转变换和置换,可证明变换后的激活值动态范围减小。
方差分析:
假设原始激活值的方差为 ( \sigma^2 ),旋转变换 ( \mathbf{R} ) 是正交矩阵,置换 ( \mathbf{P} ) 是排列矩阵,两者均不改变整体方差,但重新分配方差到各通道。通过分散异常值,每个通道的方差降低,从而减少量化步长(scale)。
数学表达:
对于任意通道 ( j ),变换后的激活值为:
[ a_j’ = \sum_{i=1}^d R_{ji} a_i ] 若异常值被分散到多个通道,每个 ( a_j’ ) 的最大值 ( \max |a_j’| ) 将小于原始最大值 ( \max |a_i| )。
6. 量化误差上界
设量化步长为 ( s = \frac{\max(\mathbf{A}”) - \min(\mathbf{A}”)}{2^b - 1} ),则最大量化误差为 ( \frac{s}{2} )。通过降低 ( \max(\mathbf{A}”) ),DuQuant直接减小了 ( s ),从而降低误差上界。
总结
DuQuant的数学核心在于:
- 旋转变换:通过分块对角正交矩阵分散异常值,优化目标为最小化块内最大激活值。
- 置换操作:以Zigzag排列平衡块间异常值分布。
- 权重调整:通过逆变换保持模型输出的数学等价性。
- 理论保证:降低激活值的动态范围和方差,减小量化步长及误差。
该方法通过线性变换的数学性质,在不改变模型功能的前提下,显著提升了量化效果。
Language Model Head
在语言模型(尤其是基于Transformer的模型)中,Language Model Head(LM Head) 和 预测头(Prediction Head) 是紧密相关的概念,但它们的定义和用途略有不同。以下是具体解释:
1. Language Model Head(LM Head)
定义:
LM Head 是语言模型中用于生成下一个token的概率分布的最后一层神经网络。它将模型输出的隐藏状态(hidden states)映射到词汇表空间,从而预测下一个token。功能:
- 输入:模型最后一层的隐藏状态(例如,GPT中每个位置的隐藏向量)。
- 输出:词汇表中每个token的概率分布(
logits),通过Softmax归一化后得到概率。 - 例如,在自回归生成(如GPT)中,LM Head 根据当前位置的隐藏状态预测下一个token。
结构:
通常是一个线性层(nn.Linear),将隐藏状态维度(如d_model=768)投影到词汇表维度(如vocab_size=50,000)。# 伪代码示例(如GPT的LM Head) hidden_states = transformer_outputs.last_hidden_state # [batch, seq_len, d_model] logits = lm_head(hidden_states) # [batch, seq_len, vocab_size]典型应用场景:
- 语言模型预训练(如GPT的Next Token Prediction)。
- 文本生成(如对话、续写)。
2. 预测头(Prediction Head)
定义:
预测头是一个广义概念,指任何附加在模型主体上用于特定任务的输出层。不同的任务需要不同的预测头。功能与类型:
预测头类型 任务 输出结构 LM Head 语言建模 词汇表概率分布 分类头 文本分类 类别标签概率分布 序列标注头 命名实体识别(NER) 每个token的类别概率 跨度预测头 问答(如SQuAD) 答案起始/结束位置的概率 潜在空间映射头 潜在推理(如Coconut) 连续潜在状态的生成或解码 结构:
根据任务需求设计,例如:- 分类头:线性层 + Softmax。
- 问答头:两个线性层分别预测起始和结束位置。
- 潜在空间头:可能包含多层感知机(MLP)或投影矩阵。
3. LM Head 与预测头的关系
包含关系:
LM Head 是预测头的一种特定类型,专用于语言建模任务(预测下一个token)。其他预测头则服务于不同任务(如分类、问答)。灵活性与复用性:
- 在预训练-微调范式(Pretrain-Finetune)中,LM Head 通常在预训练阶段使用,而微调时会替换为任务相关的预测头(如分类头)。
- 某些模型(如T5、UniLM)通过共享LM Head实现多任务生成,此时LM Head同时充当任务通用预测头。
潜在空间推理中的特殊设计:
在论文提到的Coconut模型中,潜在模式(latent mode)可能引入特殊的预测头:- 当模型切换到潜在推理时,可能使用一个额外的头(如MLP)生成连续潜在状态(
h_t)。 - 切换回语言模式时,继续使用LM Head生成离散token。
- 当模型切换到潜在推理时,可能使用一个额外的头(如MLP)生成连续潜在状态(
4. 直观对比
| 概念 | 用途 | 输入 | 输出 | 示例场景 |
|---|---|---|---|---|
| LM Head | 生成下一个token | 隐藏状态(如GPT) | 词汇表概率分布 | 文本生成、预训练 |
| 分类头 | 文本分类 | [CLS]位置的隐藏状态 | 类别标签概率 | 情感分析、意图识别 |
| 潜在空间映射头 | 生成连续潜在状态 | 隐藏状态 + 控制信号 | 连续向量(如h_t) | Coconut的潜在推理阶段 |
总结
- Language Model Head 是预测头的一种,专门用于语言建模任务(预测离散token)。
- 预测头是更广义的概念,涵盖所有任务相关的输出层设计,包括但不限于LM Head。
- 在复杂模型(如Coconut)中,预测头可能动态切换(如语言模式→潜在模式),以支持不同推理阶段的需求。

